Помогите решить задачу (Геометрия 8 класс)
Приложения:
Ответы на вопрос
Ответил vasilsenkin
0
Для решения такой задачи используется одно из свойств биссектрисы треугольника. Кроме общеизвестного факта, что биссектриса делит угол пополам есть другой, знакомый не всем: биссектриса делит противоположную сторону на отрезки, пропорциональные сторонам треугольника, между которыми она проведена.
Но это чуть позже.
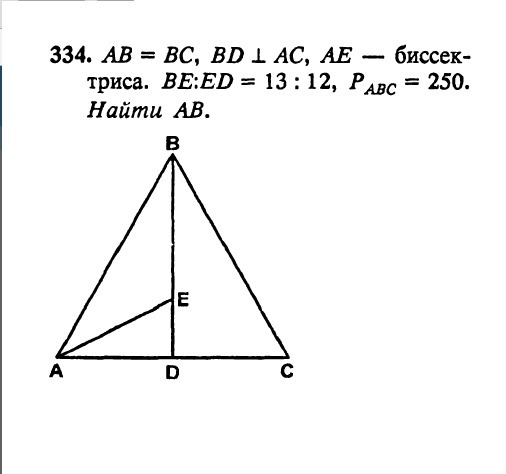
АВ=ВС - треугольник равнобедренный. BD - высота, проведенная к основанию является медианой и биссектрисой.
AD и AB являются сторонами треугольника, в котором проведена биссектриса. Здесь не обойтись без пропорции:
AB : AD = BE : ED = 13 : 12. Значит
![13*AD=12*AB \
AD= frac{12}{13} AB \](https://tex.z-dn.net/?f=13%2AAD%3D12%2AAB+%5C+%0AAD%3D+frac%7B12%7D%7B13%7D+AB+%5C+%0A%0A "13*AD=12*AB \
AD= frac{12}{13} AB \")
Выполняем подстановку в формулу периметра
![2*AB+2* frac{12}{13} *AB=AB(2+ frac{24}{13} )=AB* frac{50}{13} \
frac{50}{13} AB=250 \
AB=250: frac{50}{13} \
AB=250* frac{13}{50} \
AB=65](https://tex.z-dn.net/?f=2%2AAB%2B2%2A+frac%7B12%7D%7B13%7D+%2AAB%3DAB%282%2B+frac%7B24%7D%7B13%7D+%29%3DAB%2A+frac%7B50%7D%7B13%7D++%5C+%0A+frac%7B50%7D%7B13%7D+AB%3D250+%5C+%0AAB%3D250%3A+frac%7B50%7D%7B13%7D++%5C+%0AAB%3D250%2A+frac%7B13%7D%7B50%7D+%5C+%0AAB%3D65 "2*AB+2* frac{12}{13} *AB=AB(2+ frac{24}{13} )=AB* frac{50}{13} \
frac{50}{13} AB=250 \
AB=250: frac{50}{13} \
AB=250* frac{13}{50} \
AB=65")
Проверяем. AD = 65*12/13 = 60. АС = 120. Р = 65+65+120=250.
Ответ: АВ=65.
Но это чуть позже.
АВ=ВС - треугольник равнобедренный. BD - высота, проведенная к основанию является медианой и биссектрисой.
AD и AB являются сторонами треугольника, в котором проведена биссектриса. Здесь не обойтись без пропорции:
AB : AD = BE : ED = 13 : 12. Значит
Выполняем подстановку в формулу периметра
Проверяем. AD = 65*12/13 = 60. АС = 120. Р = 65+65+120=250.
Ответ: АВ=65.
Новые вопросы
Английский язык,
2 года назад
Русский язык,
2 года назад
Математика,
8 лет назад
История,
9 лет назад