Помогите решить задачи по алгебре !!!!!
Приложения:
Ответы на вопрос
Ответил mefody66
0
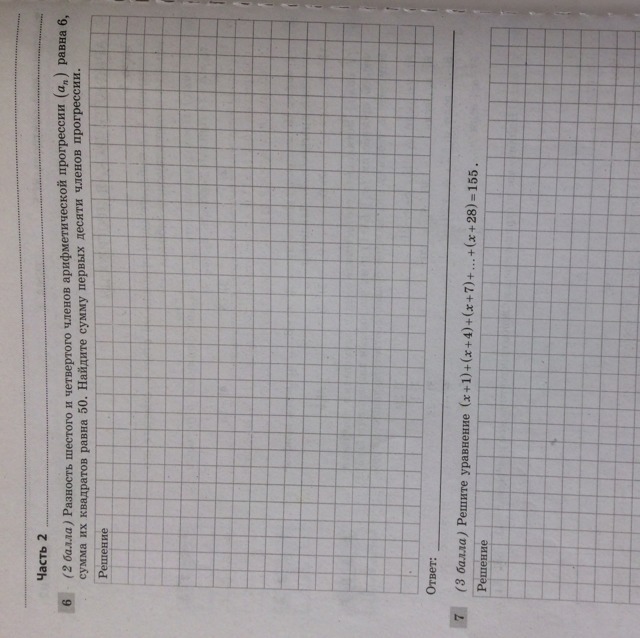
1 Задача.
{ a6 - a4 = a1 + 5d - a1 - 3d = 2d = 6; d = 3
{ a6^2 + a4^2 = (a1 + 5d)^2 + (a1 + 3d)^2 = (a1+15)^2 + (a1+9)^2 = 50
a1^2 + 30*a1 + 225 + a1^2 + 18*a1 + 81 = 2a1^2 + 48*a1 + 306 = 50
2a1^2 + 48*a1 + 256 = 0
a1^2 + 24*a1 + 128 = 0
(a1 + 16)(a1 + 8) = 0
1) a1 = -16; d = 3; a4 = a1+3d = -16+9 = -7; a6 = a1+5d = -16+15 = -1
a10 = a1 + 9d = -16 + 9*3 = -16 + 27 = 11
S(10) = (a1 + a10)*10/2 = (-16 + 11)*5 = -5*5 = -25
2) a1 = -8; d = 3; a4 = a1+3d = -8+9 = 1; a6 = a1+5d = -8+15 = 7
a10 = a1 + 9d = -8 + 9*3 = -8 + 27 = 19
S(10) = (a1 + a10)*10/2 = (-8 + 19)*5 = 11*5 = 55
2 Задача.
(x+1) + (x+4) + (x+7) + ... + (x+28) = 155
В скобках стоят члены арифметической прогрессии, a1 = x+1; d = 3.
Количество скобок равно n = (28 - 1)/3 + 1 = 27/3 + 1 = 9 + 1 = 10
S(10) = (x+1 + x+28)*10/2 = (2x + 29)*5 = 155
2x + 29 = 155/5 = 31
2x = 31 - 29 = 2
x = 1
{ a6 - a4 = a1 + 5d - a1 - 3d = 2d = 6; d = 3
{ a6^2 + a4^2 = (a1 + 5d)^2 + (a1 + 3d)^2 = (a1+15)^2 + (a1+9)^2 = 50
a1^2 + 30*a1 + 225 + a1^2 + 18*a1 + 81 = 2a1^2 + 48*a1 + 306 = 50
2a1^2 + 48*a1 + 256 = 0
a1^2 + 24*a1 + 128 = 0
(a1 + 16)(a1 + 8) = 0
1) a1 = -16; d = 3; a4 = a1+3d = -16+9 = -7; a6 = a1+5d = -16+15 = -1
a10 = a1 + 9d = -16 + 9*3 = -16 + 27 = 11
S(10) = (a1 + a10)*10/2 = (-16 + 11)*5 = -5*5 = -25
2) a1 = -8; d = 3; a4 = a1+3d = -8+9 = 1; a6 = a1+5d = -8+15 = 7
a10 = a1 + 9d = -8 + 9*3 = -8 + 27 = 19
S(10) = (a1 + a10)*10/2 = (-8 + 19)*5 = 11*5 = 55
2 Задача.
(x+1) + (x+4) + (x+7) + ... + (x+28) = 155
В скобках стоят члены арифметической прогрессии, a1 = x+1; d = 3.
Количество скобок равно n = (28 - 1)/3 + 1 = 27/3 + 1 = 9 + 1 = 10
S(10) = (x+1 + x+28)*10/2 = (2x + 29)*5 = 155
2x + 29 = 155/5 = 31
2x = 31 - 29 = 2
x = 1
Новые вопросы
Математика,
1 год назад
Алгебра,
1 год назад
Математика,
7 лет назад
Математика,
7 лет назад
Математика,
8 лет назад