помогите решить задачи

Ответ:

1)5

2)16

3)14

4)60°, 60°

5)4,5, 90°

6)10

7)20°

8)65°, 90°

Объяснение:

1)∠B=60⇒∠A=90°-60°=30°⇒BC=10/2=5

2)ΔBCD - равнобедренный, т.к. в нем один угол 90°, а другой - 45°. Значит DC=DB=8. По т. Пифагора BC=√(8²+8²)=8√2

По тем же причинам ΔABC - тоже равнобедренный, т.е. AC=BC=8√2.

По т. Пифагора AB=√(8²×2+8²×2)=√(8²×4)=8×2=16

3)В ΔBEC ∠E=60°⇒B=90°-60°=30°⇒BE=7×2=14. По т. Пифагора BC=√(14²-7²)=7√3

В ΔABC ∠A=30°⇒AB=2×7√3=14√3. По т. Пифагора AC=√(14²×3-7²×3)=21. AE=AC-EC=21-7=14

4)AB=AD⇒ΔABD - равнобедренный ⇒∠B=∠D. В прямоугольном ΔACD катет CD равен половине гипотенузы AD⇒∠DAC=30°⇒∠ADC=90°-30°=60°=∠B=∠D.

5)CK - высота, значит ∠C=90°.

∠CKE=90°-∠CEK=90°-(90-∠EFK)=∠EFK=180°-150°=30°⇒CE=9/2=4,5

6)∠B=180°-150°=30°⇒∠A=90°-30°=60°. AA1 - биссектриса⇒∠CAA1=∠A1AB=60°/2=30°⇒CA1=20/2=10

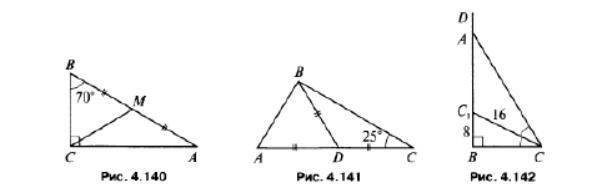
7)CM - медиана в прямоугольном треугольнике, значит она равна половине гипотенузы, т.е. BM=MC, т.е. ΔBMC - равнобедренный, значит ∠BCM=∠B=70°⇒∠MCA=90°-∠B=90°-70°=20°

8)BD=DC⇒ΔBDC - равнобедренный⇒∠C=∠DBC=25°⇒∠DBC=180°-2×25°=130°⇒∠ADB=180°-130°=50°. Треугольник ABD также равнобедренный, т.е. ∠A=∠ABD, при это сумма ∠A и ∠ABD равна 180°-50°=130°, т.е. ∠A+∠ABD=2∠A=130°⇒∠A=∠ABD=130°/2=65°, тогда ∠ABC=∠ABD+∠BDC=65°+25°=90°