помогите решить уравнения!!!
Приложения:
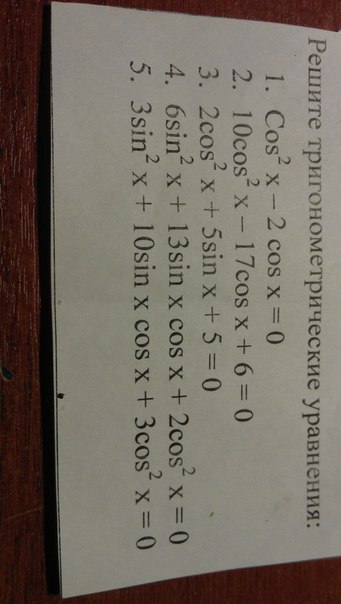
Ответы на вопрос
Ответил dnepr1
0
1) cos² x - 2cos x = 0
cos x(cos x- 2) = 0 cos x₁ = 0 x₁ = Arc cos 0 = 2kπ+-π/2.
cos x₂ = 2 - не принимается.
2) 10cos² x - 17cos x + 6 = 0
Примем cos x = а, тогда 10а² - 17а +6 = 0
D = 49 a₁ = 12 a₂ = 0.5
a₁ не принимается, cos x₂ = 0,5
х₂ = Arc cos(0,5) = 2kπ+-π/3.
3) 2cos² x + 5sin x + 5 = 0 cos²x = 1 - sin²x
2*(1 - sin²x) + 5sin x + 5 = 0 2sin²x + 5sin x + 7 = 0
Примем sin x = а, тогда -2а² + 5а +7 = 0
D = 81 a₁ = -1 a₂ = 3,5 - не принимается.
sin x₁ = -1 х₁ = Arc sin(-1) = kπ-(-1)^k*π/2.
4) 6sin² x+13sin x * cos x + 2cos² x = 0.
Разделим обе части уравнения на cos² x и получим:
6tg² x + 13tg x + 2 = 0 D = 121
tg x₁ = -1/6 x₁ = Arc tg(-1/6) = kπ+-(-0,16515) - радиан.
tg x₂ = -2 x₂ = Arc tg(-2) = kπ+-(-1,10715) - радиан.
5) 3sin² x + 10sin x*cos x + 3cos² x = 0
Разделим обе части уравнения на cos² x и получим:
3tg² x + 10tg x + 3 = 0 D = 64
tg x₁ = -1/3 x₁ = Arc tg(-1/3) = kπ+-(-0,32175) - радиан.
tg x₂ = -3 x₂ = Arc tg(-3) = kπ+-(-1,24905) - радиан.
cos x(cos x- 2) = 0 cos x₁ = 0 x₁ = Arc cos 0 = 2kπ+-π/2.
cos x₂ = 2 - не принимается.
2) 10cos² x - 17cos x + 6 = 0
Примем cos x = а, тогда 10а² - 17а +6 = 0
D = 49 a₁ = 12 a₂ = 0.5
a₁ не принимается, cos x₂ = 0,5
х₂ = Arc cos(0,5) = 2kπ+-π/3.
3) 2cos² x + 5sin x + 5 = 0 cos²x = 1 - sin²x
2*(1 - sin²x) + 5sin x + 5 = 0 2sin²x + 5sin x + 7 = 0
Примем sin x = а, тогда -2а² + 5а +7 = 0
D = 81 a₁ = -1 a₂ = 3,5 - не принимается.
sin x₁ = -1 х₁ = Arc sin(-1) = kπ-(-1)^k*π/2.
4) 6sin² x+13sin x * cos x + 2cos² x = 0.
Разделим обе части уравнения на cos² x и получим:
6tg² x + 13tg x + 2 = 0 D = 121
tg x₁ = -1/6 x₁ = Arc tg(-1/6) = kπ+-(-0,16515) - радиан.
tg x₂ = -2 x₂ = Arc tg(-2) = kπ+-(-1,10715) - радиан.
5) 3sin² x + 10sin x*cos x + 3cos² x = 0
Разделим обе части уравнения на cos² x и получим:
3tg² x + 10tg x + 3 = 0 D = 64
tg x₁ = -1/3 x₁ = Arc tg(-1/3) = kπ+-(-0,32175) - радиан.
tg x₂ = -3 x₂ = Arc tg(-3) = kπ+-(-1,24905) - радиан.
Новые вопросы