Алгебра, вопрос задал asgeras28 , 7 лет назад

Помогите решить уравнение
{x/y+y/x=5,2
{x^2-y^2=24

Приложения:

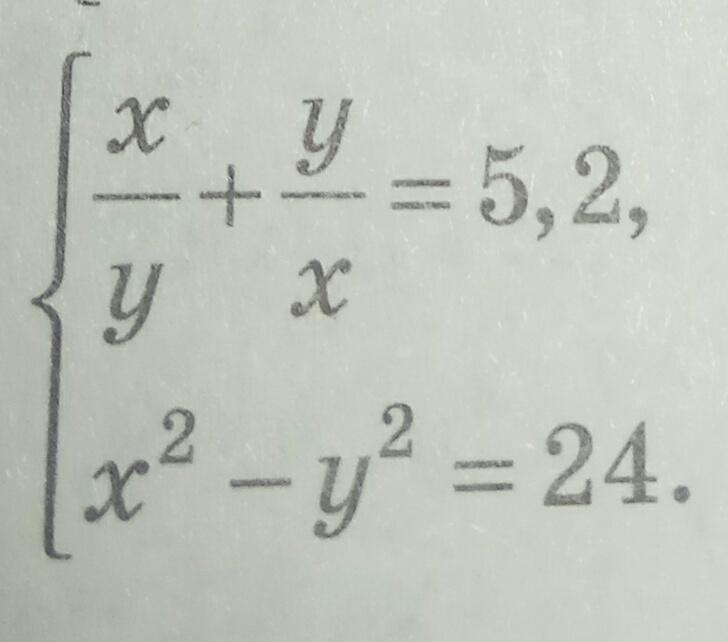
Ответы на вопрос

Ответил Universalka

0

Преобразуем первое уравнение, сделав замену :

$frac{x}{y}=a\\frac{y}{x}=frac{1}{a}\\a+frac{1}{a}=5,2\\a^{2}-5,2a+1=0,aneq0\\D=(-5,2)^{2}-4*1=27,04-4=23,04=4,8^{2}\\a_{1}=frac{5,2+4,8}{2}=5\\a_{2} =frac{5,2-4,8}{2}=0,2=frac{1}{5}$

$1)frac{x}{y}=5\\x=5y\\left { {{x=5y} atop {x^{2}-y^{2}=24}} right.\\left { {{x=5y} atop {25y^{2}-y^{2}=24}} right.\\left { {{x=5y} atop {24y^{2}=24 }} right.\\left { {{x=5y} atop {y^{2}=1 }} right.\\y_{1} =1;x_{1}=5\\y_{2} =-1;x_{2}=-5$

$2)frac{x}{y}=frac{1}{5}\\y=5x\\left { {{y=5x} atop {x^{2}-25x^{2} =24 }} right.\\left { {{y=5x} atop {-24x^{2}=24 }} right.\\left { {{y=5x} atop {x^{2}=-1<0 }} right.$

Решений нет

Ответ : (5 ; 1) , (- 5 ; - 1)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Озаглавить отрывок и запиши названия. Из всех деревьев.русского леса милее всех мне наша берёза.хороши и чисты берёзовые светлые рощи есть в русской природе радостный когда на берёзах начинает...

Русский язык, 1 год назад

укажите способ образования слова бесконечности...

Химия, 7 лет назад

Можно название продуктов...

Математика, 7 лет назад

помогите пж!!!!!!!!!!!!!!!!!!!! Расстояние между городами A и B на карте, масштаб которой является 1 : 1 000 000, 4 cm. Сколько расстояние между этими городами в природе и насколько велика -- на...

Математика, 8 лет назад

Разность двух чисел на 23 меньше первого из них.Найдите второе число...

Математика, 8 лет назад

Отметьте на координатномлуче точки, соответствующие числам 1, 3, 5, если единичный отрезок равен 1 см. Начертите ещё два координатных луча и отметьте на них эти же числа, выбрав за длину ед. Отрезка:...