Помогите решить уравнение по алгебре
Приложения:
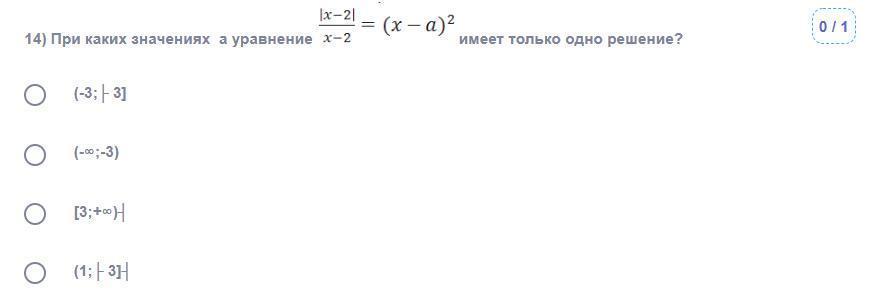
Ответы на вопрос
Ответил nafanya2014
2
Если x-2 < 0 ,т. е x < 2
|x-2|=-(x-2)
поэтому уравнение принимает вид:
-Уравнение не имеет решений
Если x-2 >0 ,т. е x > 2
|x-2|=x-2
поэтому уравнение принимает вид:
или
или
Чтобы выполнялось требование задачи, один из найденных корней не должен удовлетворять условию x > 2
Так как
то
О т в е т. 4) (1; 3]
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Окружающий мир,
2 года назад
Другие предметы,
2 года назад
Математика,
7 лет назад