Алгебра, вопрос задал Аноним , 9 лет назад

помогите решить уравнение

Приложения:

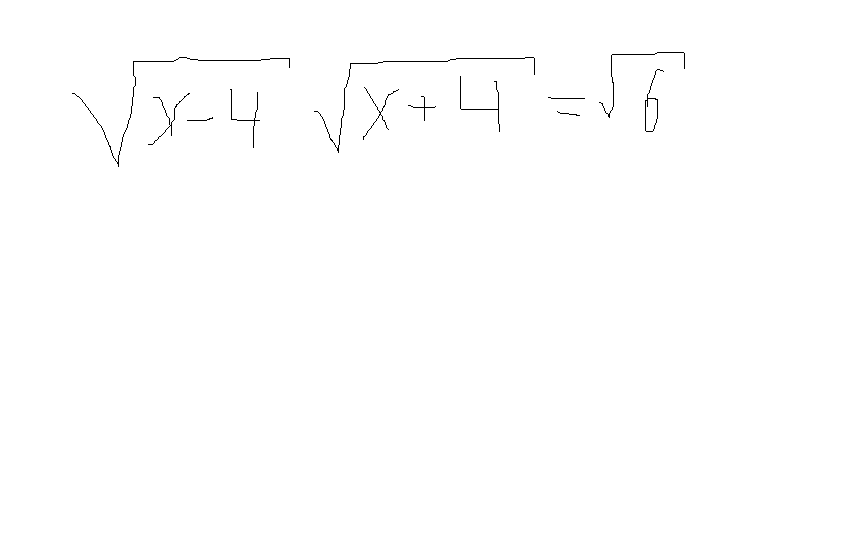
Ответы на вопрос

Ответил Artem112

$sqrt{x-4}sqrt{x+4}=sqrt{6}$

ОДЗ:

$left{begin{array}{l} x-4 geq 0 \ x+4 geq 0 end{array}Rightarrow left{begin{array}{l} x geq 4 \ x geq -4 end{array} Rightarrow x geq 4$

Решаем уравнение:

$sqrt{x-4}sqrt{x+4}=sqrt{6}$

Произведение корней есть корень из произведения:

$sqrt{(x-4)(x+4)}=sqrt{6}$

$sqrt{x^2-16}=sqrt{6}$

Возводим обе части уравнения в квадрат:

$x^2-16=6$
$x^2=6+16$
$x^2=22$
$x_1=sqrt{22}$

$x_2=-sqrt{22}</strong><span><strong>$ - не удовлетворяет ОДЗ

Ответ: $sqrt{22}$

Предыдущий вопрос

Новые вопросы

Право, 6 лет назад

Английский язык, 6 лет назад

Биология, 9 лет назад

Литература, 9 лет назад

Физика, 9 лет назад

Химия, 9 лет назад