Алгебра, вопрос задал azazina , 8 лет назад

Помогите решить тригонометрическое
уравнение! sin3x/1+2cos2x=0
(Файл прикреплён)

Приложения:

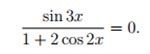
Ответы на вопрос

Ответил KuOV

Ответ: x = πm, m∈Z

Объяснение:

$dfrac{sin3x}{1+2cos2x}=0$

$left{begin{array}{ll}sin3x=0\1+2cos2xneq 0end{array}$

1. Решим первое уравнение:

sin 3x = 0

3x = πn, n∈Z

$x=dfrac{pi n}{3}$ , n∈Z

2. Решим уравнение

1 + 2cos 2x = 0

$cos2x=-frac{1}{2}$

$2x=pm arccos(-frac{1}{2})+2pi k$ ,

$2x=pm (pi -arccos(frac{1}{2}))+2pi k$ ,

$2x=pm (pi -frac{pi }{3})+2pi k$ ,

$2x=pm frac{2pi }{3}+2pi k$ ,

$x=pm frac{pi }{3}+pi k$ , k∈Z

Итак,

$left{ begin{array}{ll}x=frac{pi n}{3},\xneq pm frac{pi }{3}+pi kend{array}$

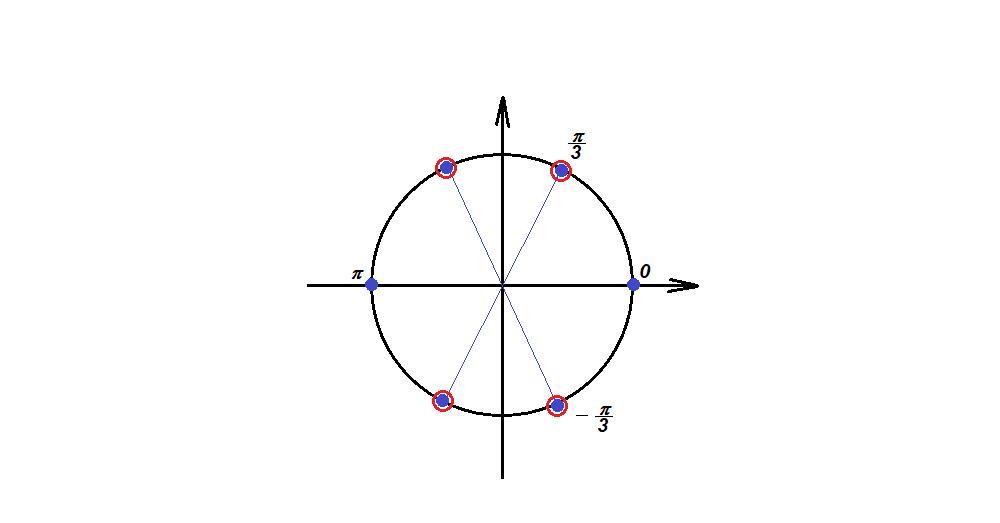
Корни первого уравнения отмечены на окружности синими точками, значения х, при которых знаменатель равен нулю, обведены красными, значит решением уравнения будет

x = πm, m∈Z

Приложения: