Алгебра, вопрос задал Akvamarin118 , 8 лет назад

Помогите решить: $frac{4}{x-1} - frac{4}{x+1} =1$

Ответы на вопрос

Ответил Аноним

I hope this helps you

Приложения:

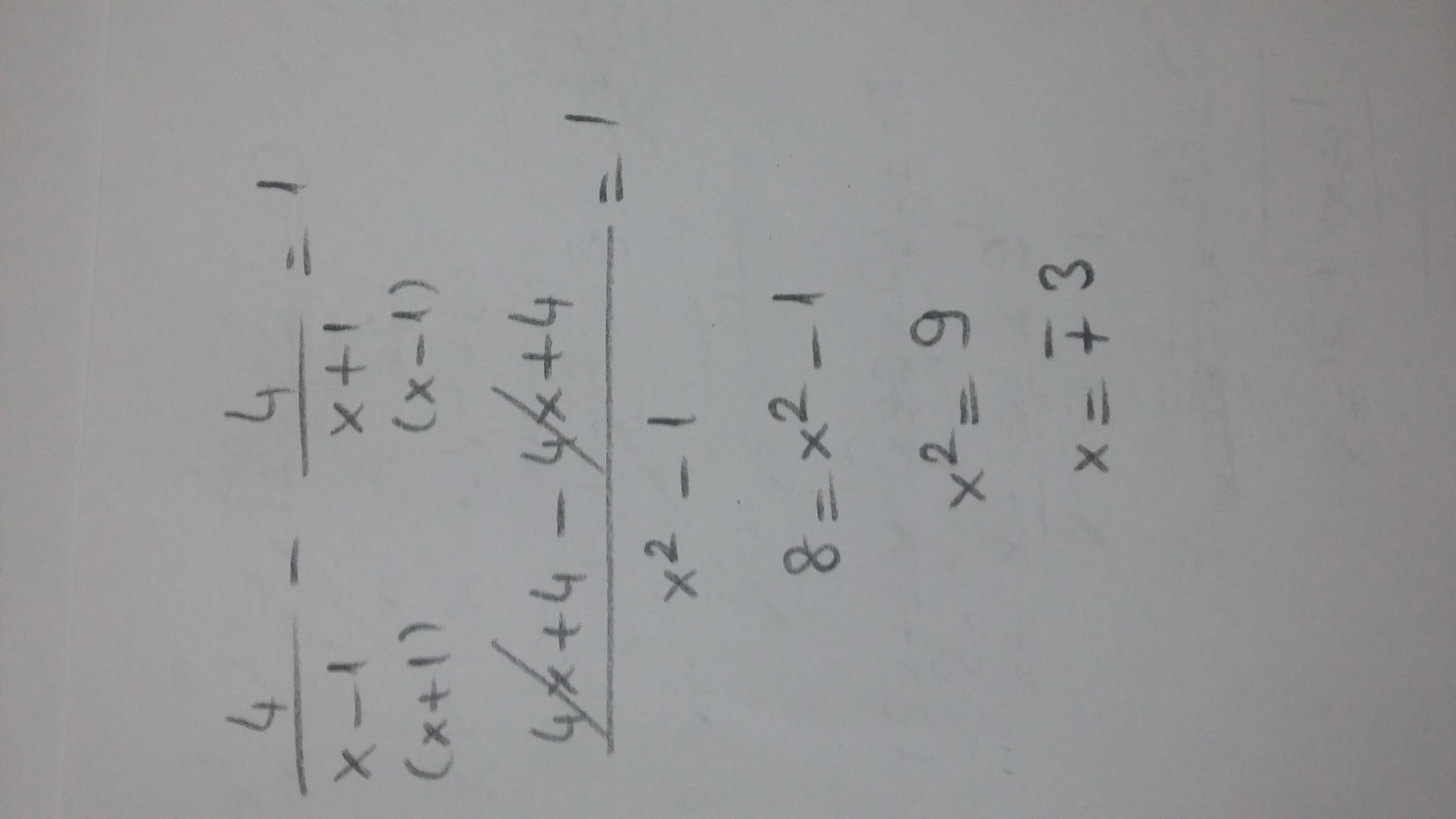
Ответил yugolovin

Хотелось бы в решении иметь ограничение по ОДЗ. Хотя задача настолько простая, что Вы можете не согласиться с этим))

Ответил F1staShka

$frac{4}{x-1} - frac{4}{x+1} =1 \ frac{4}{x-1} - frac{4}{x+1} -1=0 \ frac{4(x+1)-4(x-1)-(x-1)(x+1)}{(x-1)(x+1)} =0 \ frac{4x+4-4x+4- x^{2} +1}{(x+1)(x-1)} = frac{- x^{2} +9}{(x+1)(x-1)} = frac{- x^{2} +9}{ x^{2} -1} \ x neq +-1 \ - x^{2} +9=0 \ x^{2} =9 \ x=+-3$

Приложения:

Предыдущий вопрос

Следующий вопрос

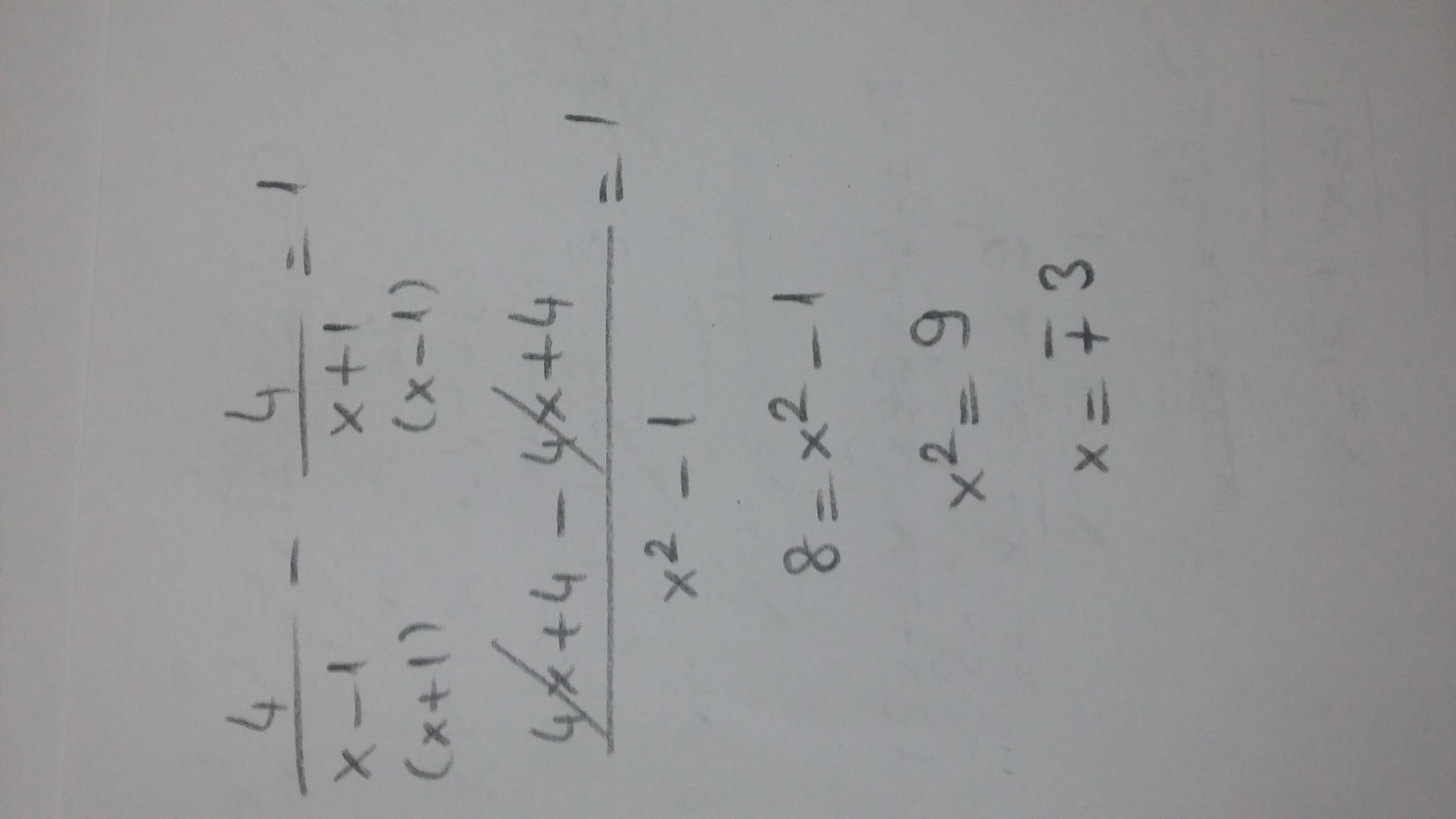
Новые вопросы

Информатика, 2 года назад

Написать программу на питон Гуляя по стройке, Лёша загляделся на только что построенную стену. Поскольку он очень любит математику, он решил посчитать количество кирпичей в ней. Однако настолько...

Биология, 2 года назад

СРОЧНО, БИОЛОГИЯ,❗❗❗ НАЙДИТЕ СООТВЕТСТВИЯ ТКАНИ И ОРГАНИЗМЫ СМОТРЕТЬ НА ФОТО☜ ...

Геометрия, 8 лет назад

Помогите доказать пожалуйста подробнее. Дано: AB || CD Доказать: BF = ED (фото)...

Математика, 8 лет назад

Периметр трикутника АВС, описаного навколо кола, дорівнює 36 см. Точка дотику кола зі стороною ВС ділить її у відношенні 2:5, рахуючи від точки В, а точка дотику зі стороною АС віддалена від точки А...

Информатика, 9 лет назад

Как устроены колонки...

Математика, 9 лет назад

найдите значение выражение:1/4*4/9;1/7*2 1/3;2 2/5*5/6;(1/5+2/15)*3/4;(1/2-1/3)*6 заранее спасибо...