Математика, вопрос задал dam19ballov , 2 года назад

Помогите решить срочно,прошу

Приложения:

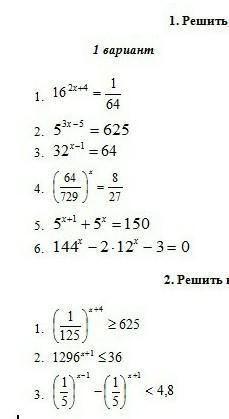
Ответы на вопрос

Ответил natalyabryukhova

Ответ:

Пошаговое объяснение:

УРАВНЕНИЯ:

Если степени равны и равны их основания, то показатели тоже равны.

$1.\;16^{2x+4}=\frac{1}{64}\\(2^4)^{2x+4}=2^{-6}$

Вспомним: $(a^n)^m=a^{nm}$

$2^{8x+16}=2^{-6}\\8x+16=-6\\8x=-22\\x=-\frac{22}{8} \\x=-2\frac{3}{4}$

Ответ: $-2\frac{3}{4}$

$2.\;5^{3x-5}=625\\5^{3x-5}=5^4\\3x-5=4\\3x=9\\x=3$

Ответ: 3

$3. \;32^{x-1}=64\\(2^5)^{x-1}=2^6\\2^{5x-5}=2^6\\5x-5=6\\5x=11\\x=\frac{11}{5}\\x= 2\frac{1}{5}$

Ответ: $2\frac{1}{5}$

$4.\;(\frac{64}{729})^x=\frac{8}{27}\\\\ ((\frac{8}{27})^2)^x =\frac{8}{27}\\\\(\frac{8}{27})^{2x}=(\frac{8}{27})^1\\2x=1\\x=\frac{1}{2}$

Ответ: $\frac{1}{2}$

$5.\;5^{x+1}+5^x=150$

Вспомним: $a^{m+n}=a^m*a^n$

$5^1*5^x+5^x=150\\(5+1)*5^x=150\\5^x=25\\5^x=5^2\\x=2$

$6.\;144^x-2*12^x-3=0\\(12^2)^x-2*12^x-3=0\\12^{2x}-2*12^x-3=0$

Выполним замену:

$12^x=t,\;\;\;t>0\\t^2-2t-3=0$

По теореме Виета:

$t_1=3;\;\;\;t_2=-1(ne\;podhodit,\;t>0)\\12^x=3\\x=log_{12}3$

Ответ: $log_{12}3$

НЕРАВЕНСТВА:

$a^{f(x)}>a^{g(x)}$

Если a>1, то f(x)>g(x)

Если 0<а<1, то f(x)<g(x)

Вспомним: Если обе части неравенства умножить (разделить) на отрицательное число, то знак неравенства перевернется.

$1.\;(\frac{1}{125})^{x+4}\geq 625\\\\(5^{-3})^{x+4} \geq 5^4\\\\5^{-3x-12}\geq 5^4\\-3x-12\geq 4\\-3x\geq 16\\x\leq -\frac{16}{3}\\x\leq -5\frac{1}{3}$

Ответ: x∈(-∞; -5]

$2.\;1296^{x+1}\leq 36\\(36^2)^{x+1}\leq 36\\(36)^{2x+2}\leq 36\\2x+2\leq 1\\2x\leq -1\\x\leq -\frac{1}{2}$

Ответ: x∈(-∞; -0,5]

$3.\;(\frac{1}{5})^{x-1}-(\frac{1}{5})^{x+1}<4,8\\\\(\frac{1}{5} )^{-1} *(\frac{1}{5})^x -(\frac{1}{5} )^{1} *(\frac{1}{5})^x <4,8\\\\5*(\frac{1}{5})^x -\frac{1}{5}*(\frac{1}{5})^x <4,8\;\;\;|*5\\\\25*(\frac{1}{5})^x -(\frac{1}{5})^x <24\\24*(\frac{1}{5})^x <24\\\\(\frac{1}{5})^x <1\\(\frac{1}{5})^x <(\frac{1}{5})^0\\x>0$