Математика, вопрос задал MariSar , 7 лет назад

помогите решить систему уравнений с параметром, плиииз. . Даю 49 баллов!!!!

Приложения:

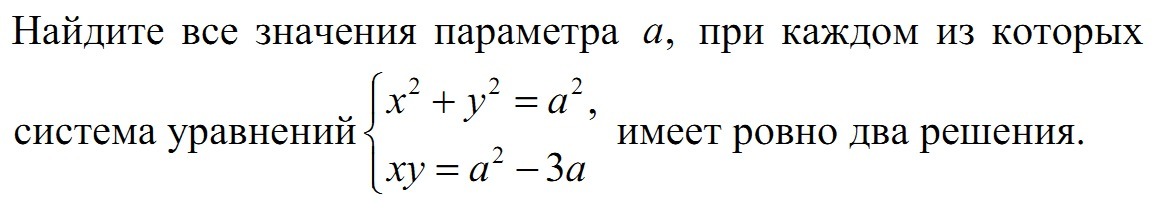
Ответы на вопрос

Ответил GeniusEnstein

$left { {{x^2+y^2=a^2} atop {xy=a^2-3a}} right.$

Если $(x;y)$ - решение, то и $(-x;-y)$ - решение

$y=frac{a^2-3a}{x}$

Т.к. при $y=0$ совпадение корней - 1 решение

$x^2+frac{(a^2-3a)^2}{x^2}-a^2=0$

Домножаем на $x^2$ :

$(x^2)^2 - a^2 cdot x^2 + (a^2-3a)^2=0$

$D=(a^2)^2-4cdot a^2 cdot (a-3)^2=a^2(a^2-4(a-3)^2)=a^2((a-(2a-6))(a+(2a-6))=a^2(a-2)(a-6)$

Если данное уравнение будет иметь:

1) 2 решения, то решениями системы будут: $(x_1;y_1); (x_2;y_2) (-x_1;-y_1); (-x_2;-y_2)$ , т.е. 4

2) 1 решение, то решениями системы будут: $(x_1;y_1) (-x_1;-y_1)$ , т.е. 2 решения как нам и надо

Решаем $D=0, a=0; a=2; a=6$

Если $a=0$ , то $x=y=0$ , чего не должно быть

Ответ: 2; 6

Ответил Красотка1259

Помогите пожалуйста : https://znanija.com/task/29708653

Новые вопросы

Русский язык, 1 год назад

Английский язык, 1 год назад

Алгебра, 7 лет назад

Математика, 7 лет назад

Математика, 8 лет назад

Химия, 8 лет назад