Алгебра, вопрос задал gamertesh2000 , 6 лет назад

ПОМОГИТЕ РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ ,ДАЮ 50 БАЛОВ !

Приложения:

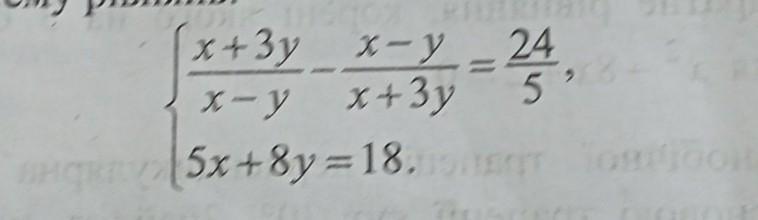
Ответы на вопрос

Ответил MatemaT123

Ответ:

$\bigg (11\dfrac{5}{11}; \ -4\dfrac{10}{11} \bigg ) \ ; \ (2; \ 1) \ ;$

Объяснение:

$D(x): \ \displaystyle \left \{ {{x-y \neq 0} \atop {x+3y \neq 0}} \right. \Leftrightarrow \left \{ {{x \neq y} \atop {x \neq -3y}} \right. ;$

Введём замену:

$\dfrac{x+3y}{x-y}=t \Rightarrow \dfrac{x-y}{x+3y}=\dfrac{1}{t};$

Перепишем первое уравнение с учётом замены:

$t-\dfrac{1}{t}=\dfrac{24}{5};$

$\dfrac{t^{2}-1}{t}=\dfrac{24}{5};$

$5t^{2}-5=24t;$

$5t^{2}-24t-5=0;$

$t^{2}-4,8t-1=0;$

Решаем уравнение по теореме Виета:

$\displaystyle \left \{ {{t_{1}+t_{2}=-(-4,8)} \atop {t_{1} \cdot t_{2}=-1}} \right. \Leftrightarrow \left \{ {{t_{1}+t_{2}=4,8} \atop {t_{1} \cdot t_{2}=-1}} \right. \Leftrightarrow \left \{ {{t_{1}=-0,2} \atop {t_{2}=5}} \right. ;$

Вернёмся к замене:

$\dfrac{x+3y}{x-y}=\dfrac{-1}{5} \quad \vee \quad \dfrac{x+3y}{x-y}=5;$

$5x+15y=y-x \quad \vee \quad x+3y=5x-5y;$

$5x+x+15y-y=0 \quad \vee \quad 5x-x-5y-3y=0;$

$6x+14y=0 \quad \vee \quad 4x-8y=0;$

$3x+7y=0 \quad \vee \quad 4x-8y=0;$

Вернёмся к системе:

$\displaystyle \left \{ {{3x+7y=0} \atop {5x+8y=18}} \right. \vee \left \{ {{4x-8y=0} \atop {5x+8y=18}} \right. \Leftrightarrow \left \{ {{15x+35y=0} \atop {-15x-24y=-54}} \right. \vee \left \{ {{4x+5x=18} \atop {5x+8y=18}} \right. \Leftrightarrow$

$\displaystyle \Leftrightarrow \left \{ {{15x+35y=0} \atop {11y=-54}} \right. \vee \left \{ {{9x=18} \atop {5x+8y=18}} \right. \Leftrightarrow \left \{ {{3x+7y=0} \atop {y=-\dfrac{54}{11}}} \right. \vee \left \{ {{x=2} \atop {10+8y=18}} \right. \Leftrightarrow$

$\displaystyle \Leftrightarrow \left \{ {{x=\dfrac{7}{3} \cdot \dfrac{54}{11}} \atop {y=-4\dfrac{10}{11}}} \right. \vee \left \{ {{x=2} \atop {8y=18-10}} \right. \Leftrightarrow \left \{ {{x=7 \cdot \dfrac{18}{11}} \atop {y=-4\dfrac{10}{11}}} \right. \vee \left \{ {{x=2} \atop {8y=8}} \right. \Leftrightarrow \left \{ {{x=\dfrac{126}{11}} \atop {y=-4\dfrac{10}{11}}} \right. \vee$

$\displaystyle \vee \left \{ {{x=2} \atop {y=1}} \right. \Leftrightarrow \left \{ {{x=11\dfrac{5}{11}} \atop {y=-4\dfrac{10}{11}}} \right. \vee \left \{ {{x=2} \atop {y=1}} \right. \ ;$