Алгебра, вопрос задал iiiiiiaaaaaaaooooo , 6 лет назад

помогите решить систему уравнений

Приложения:

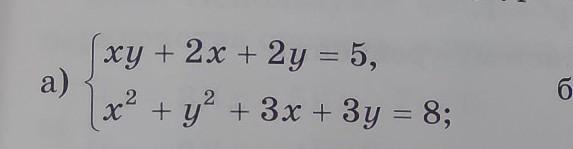
Ответы на вопрос

Ответил semavolokh

Ответ:

(1, 1)

Объяснение:

Преобразуем систему уравнений:

$\left \{ {{xy + 2(x+y)=5} \atop {(x+y)^2 -2xy + 3(x+y)=8}} \right.$

Заменим x+y = t, xy = z, затем умножим первое равенство на 2 и сложим со вторым. Получим:

$t^2 + 7t - 18 = 0$

Решив уравнение, получим t = 2; t = -9. Значения z можно найти из первого уравнения системы ( $z + 2t = 5 => z = 5 - 2t$ ). Они равны 1 и 23 соответственно.

Вернемся к изначальным переменным.

$\left \{ {{x+y=2} \atop {xy=1}} \right. \\\left \{ {{x+y=-9} \atop {xy=23}} \right. \\$

1 система) Выразим из первого равенства y. y = 2 - x, подставим во второе: x(2-x) = 1 => $x^2 -2x + 1 = 0 = > (x-1)^2 = 0 => x = 1$

Тогда y = 1.

2 система) Аналогично выразим y из первого равенства. y = -9-x. Подставив во второе, получим x(-9-x) = 23 => $x^2+9x+23 = 0$ . Здесь дискриминант отрицательный, так что действительных корней уравнение не имеет.