Алгебра, вопрос задал Petya199rus , 1 год назад

ПОМОГИТЕ РЕШИТЬ САМОСТОЯТЕЛЬНУЮ РАБОТУ ПО АЛГЕБРЕ
Тема: Дробные рациональные уравнения
Очень срочно надо! :(

Приложения:

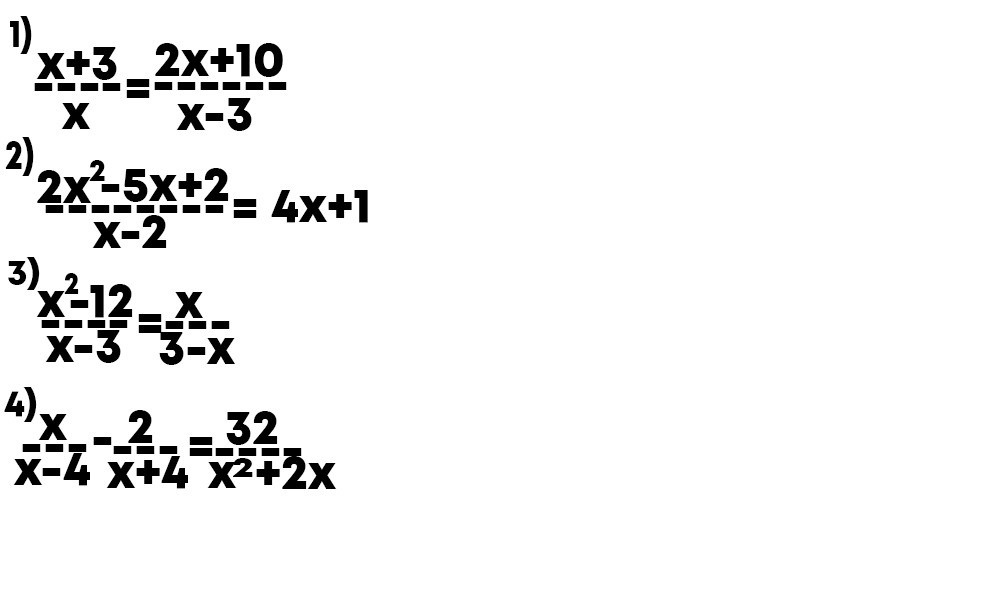
Ответы на вопрос

Ответил lilyatomach
1

Ответ:

Объяснение:

1)

\frac{x+3}{x} = \frac{2x+10}{x-3}

ОДЗ :x\neq 0, x\neq 3

\frac{x+3}{x} = \frac{2x+10}{x-3} |*x(x-3)\neq 0;\\x^{2} -9= 2x^{2} +10x;\\x^{2} +10x+9=0;\\D{_1} = 25-9=16>0\\x{_1}= -9,x{_2}= -1 \\

Ответ : -9 ; -1.

2)

\frac{2x^{2}-5 x+2}{x-2} =4x+1

ОДЗ : x\neq 2

\frac{2x^{2}-5 x+2}{x-2} =4x+1|* (x-2)\neq 0;\\2x^{2}-5 x+2= 4x^{2} - 8x+x-2;\\2x^{2} -2x-4=0|:2;\\x^{2} -x-2=0;\\D= 1+8=9>0\\x{_1} = -1\\x{_2} = 2.

ОДЗ  удовлетворяет x= - 1.

Ответ : - 1.

3)

\frac{x^{2}-12 }{x-3} = \frac{x}{3-x} ;\\\frac{x^{2}-12 }{x-3} = \frac{-x}{x-3}

ОДЗ : x\neq 3

\frac{x^{2}-12 }{x-3} = \frac{-x}{x-3} |*(x-3)\neq 0;\\x^{2} -12=-x;\\x^{2} +x-12=0;\\D= 1+48=49>0\\x{_1}= -4\\x{_2} =3

ОДЗ  удовлетворяет x= - 4.

Ответ : - 4.

4)

\frac{x}{x-4} -\frac{2}{x+4} = \frac{32}{x^{2} +2x}

ОДЗ :x\neq 4, x\neq -4, x\neq 0, x\neq -2

\frac{x^{2} +4x-2x+8}{(x-4)(x+4)} = \frac{32}{x(x+2) } ;\\\frac{x^{2} +2x+8}{(x-4)(x+4)} = \frac{32}{x(x+2) }

(x^{2} +2x+8) ( x^{2} +2x) = 32( x^{2} -16);\\x^{4} +2x^{3} +2x^{3} +4x^{2} +8x^{2} +16x= 32x^{2} -512;\\x^{4} +4x^{3} -20x^{2} +16x +512 =0;

Действительных корней нет

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика, 1 год назад
Помогите пожалуйста нужны правильные ответы...
Русский язык, 1 год назад
Срочно помогите пожалуйста!!!
Русский язык, 1 год назад
подбери однокоренные к слову целительный...
Химия, 1 год назад
Закончите уравнения CuS+O2_____ H2+O2______ MgS+O2_____ Назвать коэффициенты и полученные вещества...
Математика, 6 лет назад
Зависимомть от переменной Y от переменной X является прямой пропорциональностью.Найдите коэффицент пропорциональности. Заполните таблицу: х 16 12 0 * * у * 3 * 2 1 СРОЧНООО!!!!!!!! ДАЮ 15 БАЛЛОВ...
Алгебра, 6 лет назад
знайдіть середнє значення статистичних даних 5, 8, 11, 7, 6.