Алгебра, вопрос задал dovnara620 , 6 лет назад

помогите решить с объяснением срочно
пожалуйста

Приложения:

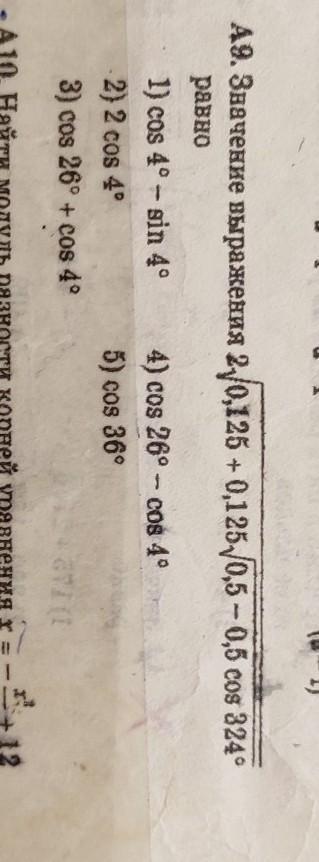
Ответы на вопрос

Ответил zinaidazina

$2\sqrt{0,125+0,125\sqrt{0,5-0,5cos324^o} } =cos36^o$

Решаем по действиям.

1) Выполним преобразования подкоренного выражения, представив угол как $324^o=2$ · $162^o$ , применим формулу косинуса двойного угла $cos2\alpha =cos^2\alpha -sin^2\alpha$ .

$0,5-0,5cos324^o=0,5[1-cos(2*162^o)]=$

$=0,5[1-cos^2162^o+sin^2162^o]=0,5[sin^2162^o+sin^2162^o]=$

$=0,5*2sin^2162^o=sin^2162^o$

2) Извлекаем корень из полученного выражения.

$\sqrt{ sin^2162^o} =sin162^o$

3) А теперь выполним преобразования общего подкоренного выражения, представив угол как $162^o=90^o+72^o$ , применим формулу приведения $sin(90^o+72^o)=cos72^o$ , а затем формулу косинуса двойного угла.