помогите решить пример
Приложения:
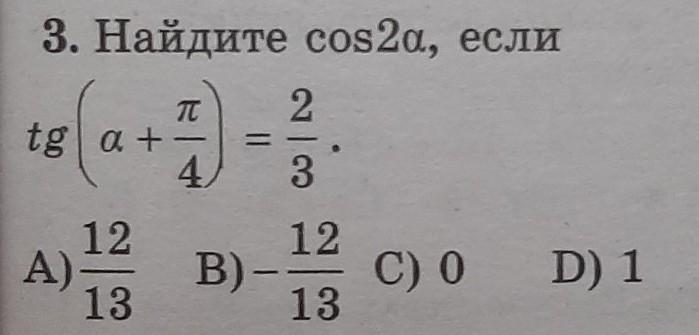
Ответы на вопрос
Ответил zinaidazina
1
Дано:
Найти
Решение:
1)
2)
3)
4)
5)
Ответ:
Новые вопросы
Английский язык,
1 год назад
Русский язык,
1 год назад
Математика,
2 года назад
Математика,
2 года назад
Физика,
7 лет назад