Помогите решить пожалуйста срочно нужно
Приложения:
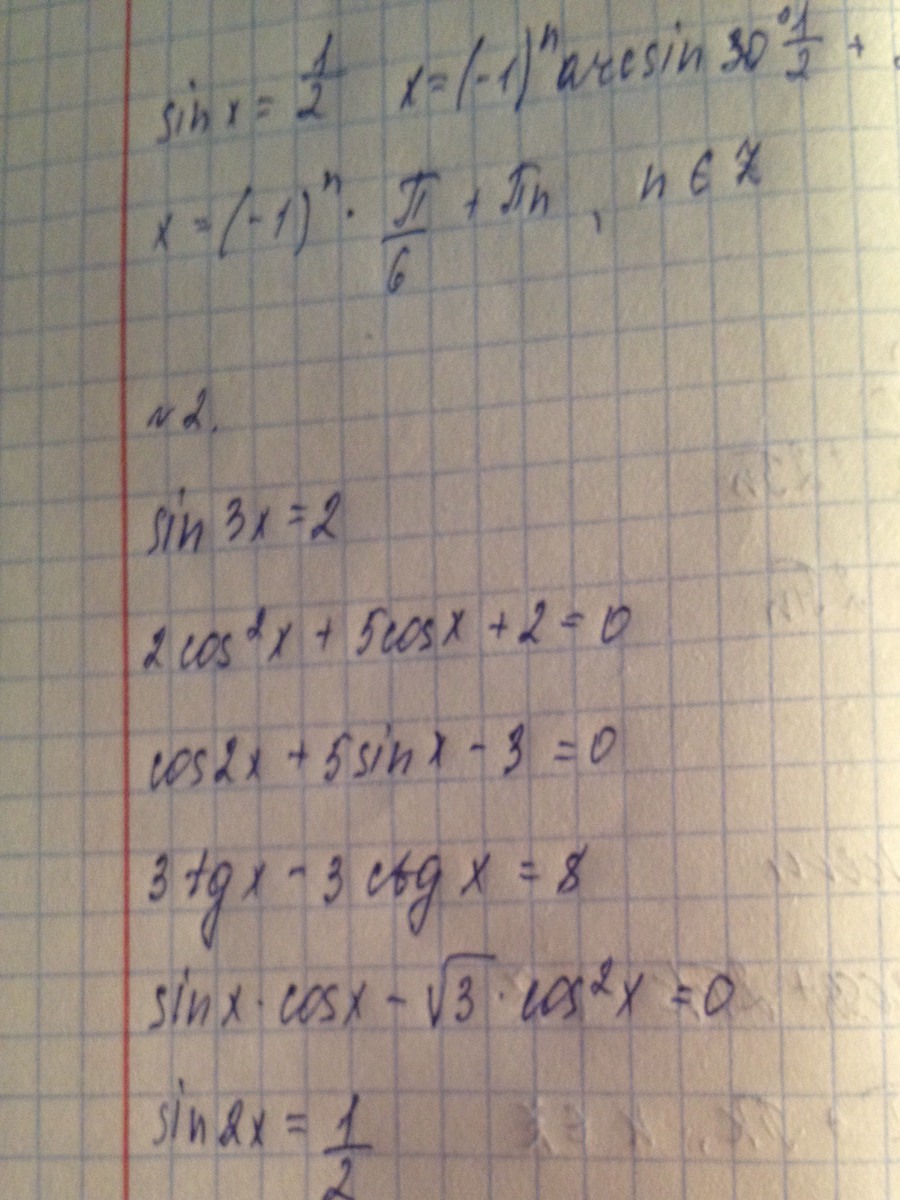
Ответы на вопрос
Ответил m11m
0
1) sin 3x=2
Так как 2∉[-1; 1], то уравнение не имеет решений.
Ответ: нет решений.
2) 2cos²x +5cosx+2=0
Пусть у=cosx
2y²+5y+2=0
D=25-4*2*2=9
y₁=5-3 = 1/2
4
y₂=5+3=2
4
При у=1/2
cosx=1/2
x=+ π/3 +2πк, к∈Z
При у=2
cosx=2
Так как 2∉[-1; 1], то уравнение не имеет корней.
Ответ: + π/3 + 2πк, к∈Z
3) cos 2x +5sinx -3=0
cos²x - sin²x +5sinx -3=0
1-sin²x -sin²x +5sinx -3=0
-2sin²x+5sinx-2=0
2sin²x-5sinx+2=0
Пусть y=sinx
2y²-5y+2=0
D=25-4*2*2=9
y₁=5-3= 1/2
4
y₂=5+3=2
4
При у=1/2
sinx=1/2
x=(-1)^k * π/6 + πk, k∈Z
При у=2
sinx=2
Так как 2∉[-1; 1], то уравнение не имеет корней.
Ответ: (-1)^k * π/6 + πk, k∈Z.
4) 3tgx - 3ctgx=8
3tgx - 3 - 8 =0
tgx
Пусть y=tgx
3y - 3 - 8=0
y
y≠0
3y²-3-8y=0
3y²-8y-3=0
D=64-4*3*(-3)=100
y₁=8-10= -2/6= -1/3
6
y₂=8+10=3
6
При у= -1/3
tgx=-1/3
x=-arctg(1/3) +πk, k∈Z
При у=3
tgx=3
x=arctg3+πk, k∈Z
Ответ: -arctg(1/3)+πk, k∈Z;
arctg 3 +πk, k∈Z.
5) sinx cosx - √3 cos²x=0
cosx (sinx -√3 cosx) =0
cosx=0
x=π/2 +πk, k∈Z
sinx - √3 cosx =0
sinx - √3 cosx = 0
cosx cosx cosx
tgx - √3 =0
tgx =√3
x=π/3 + πk, k∈Z
Ответ: π/2 +πк, к∈Z;
π/3 +πк, к∈Z.
6) sin2x=1/2
2x=(-1)^k * π/6 + πk, k∈Z
x=(-1)^k * π/12 + πk/2, k∈Z
Ответ: (-1)^k * π/12 +πk/2, k∈Z
Так как 2∉[-1; 1], то уравнение не имеет решений.
Ответ: нет решений.
2) 2cos²x +5cosx+2=0
Пусть у=cosx
2y²+5y+2=0
D=25-4*2*2=9
y₁=5-3 = 1/2
4
y₂=5+3=2
4
При у=1/2
cosx=1/2
x=+ π/3 +2πк, к∈Z
При у=2
cosx=2
Так как 2∉[-1; 1], то уравнение не имеет корней.
Ответ: + π/3 + 2πк, к∈Z
3) cos 2x +5sinx -3=0
cos²x - sin²x +5sinx -3=0
1-sin²x -sin²x +5sinx -3=0
-2sin²x+5sinx-2=0
2sin²x-5sinx+2=0
Пусть y=sinx
2y²-5y+2=0
D=25-4*2*2=9
y₁=5-3= 1/2
4
y₂=5+3=2
4
При у=1/2
sinx=1/2
x=(-1)^k * π/6 + πk, k∈Z
При у=2
sinx=2
Так как 2∉[-1; 1], то уравнение не имеет корней.
Ответ: (-1)^k * π/6 + πk, k∈Z.
4) 3tgx - 3ctgx=8
3tgx - 3 - 8 =0
tgx
Пусть y=tgx
3y - 3 - 8=0
y
y≠0
3y²-3-8y=0
3y²-8y-3=0
D=64-4*3*(-3)=100
y₁=8-10= -2/6= -1/3
6
y₂=8+10=3
6
При у= -1/3
tgx=-1/3
x=-arctg(1/3) +πk, k∈Z
При у=3
tgx=3
x=arctg3+πk, k∈Z
Ответ: -arctg(1/3)+πk, k∈Z;
arctg 3 +πk, k∈Z.
5) sinx cosx - √3 cos²x=0
cosx (sinx -√3 cosx) =0
cosx=0
x=π/2 +πk, k∈Z
sinx - √3 cosx =0
sinx - √3 cosx = 0
cosx cosx cosx
tgx - √3 =0
tgx =√3
x=π/3 + πk, k∈Z
Ответ: π/2 +πк, к∈Z;
π/3 +πк, к∈Z.
6) sin2x=1/2
2x=(-1)^k * π/6 + πk, k∈Z
x=(-1)^k * π/12 + πk/2, k∈Z
Ответ: (-1)^k * π/12 +πk/2, k∈Z
Новые вопросы
Биология,
2 года назад
Русский язык,
2 года назад
Алгебра,
9 лет назад
Химия,
9 лет назад
Математика,
9 лет назад