Помогите решить пожалуйста, даю 40 баллов

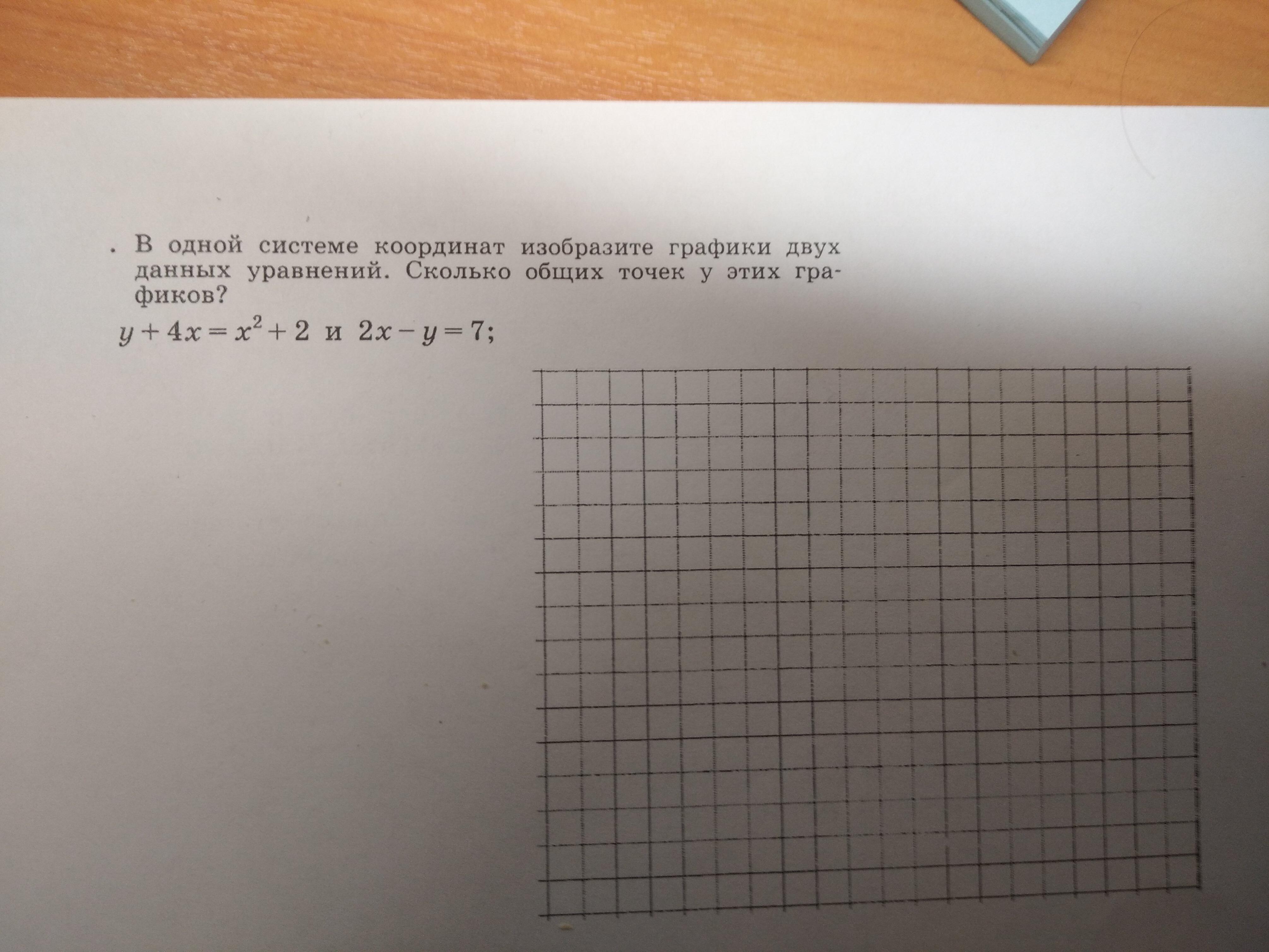
Ответы на вопрос
Ответ:
В решении.
Объяснение:
1) Преобразовать выражения в уравнения функций:
у + 4х = х² + 2 2х - у = 7
у = х² - 4х + 2; -у = 7 - 2х
у = 2х - 7;
Первое уравнение - уравнение квадратичной функции, график парабола.
Второе уравнение - уравнение линейной функции, график прямая линия.
Придать значения х, подставить в уравнение и вычислить у, записать в таблицу.
у = х² - 4х + 2 у = 2х - 7
Таблицы:
х -2 -1 0 1 2 3 4 5 6 х -1 0 1
у 14 7 -2 -1 -2 -1 2 7 14 у -9 -7 -5
Графики имеют одну общую точку (точку пересечения).
Координаты точки пересечения (3; -1).
Графики прилагаются.
2) Решить систему уравнений:
4/х² + 8/ху - 5/у² = 0
х + у = 3
Умножить первое уравнение на х²у², чтобы избавиться от дробного выражения:
4у² + 8ху - 5х² = 0
х + у = 3
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х = 3 - у
4у² + 8у(3 - у) - 5(3 - у)² = 0
4у² + 24у - 8у² - 5(9 - 6у + у²) = 0
4у² + 24у - 8у² - 45 + 30у - 5у² = 0
Привести подобные члены:
-9у² + 54у - 45 = 0
Разделить уравнение (все части) на -9 для упрощения:
у² - 6у + 5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =36 - 20 = 16 √D=4
у₁=(-b-√D)/2a
у₁=(6-4)/2
у₁=2/2
у₁=1;
у₂=(-b+√D)/2a
у₂=(6+4)/2
у₂=10/2
у₂=5;
х = 3 - у
х₁ = 3 - у₁
х₁ = 3 - 1
х₁ = 2;
х₂ = 3 - 5
х₂ = -2.
Решение системы уравнений (2; 1); (-2; 5).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
3) Решить систему уравнений:
2х² + (у - 4)² = 6
4х - ху = 2
Выразить у через х во втором уравнении, подставить выражение в первое уравнение и вычислить х:
-х(у - 4) = 2
у - 4 = -2/х
2х² + (-2/х)² = 6
2х² + 4/х² = 6
Умножить преобразованное первое уравнение на х², чтобы избавиться от дробного выражения:
2х⁴ + 4 = 6х²
2х⁴ - 6х² + 4 = 0
Разделить уравнение на 2 для упрощения:
х⁴ - 3х² + 2 = 0
Ввести новую переменную:
х² = t, получим новое уравнение:
t² - 3t + 2 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 9 - 8 = 1 √D=1
t₁=(-b-√D)/2a
t₁=(3-1)/2
t₁=2/2
t₁=1;
t₂=(-b+√D)/2a
t₂=(3+1)/2
t₂=4/2
t₂=2.
Вернуться к первоначальной переменной:
х² = t
х² = 1
х₁,₂ = ±√1
х₁,₂ = ±1;
х² = 2
х₃,₄ = ±√2
у - 4 = -2/х
у = -2/х + 4
у₁ = -2/1 + 4
у₁ = 2;
у₂ = -2/-1 + 4
у₂ = 6;
у₃ = -2/√2 + 4
Избавиться от иррациональности в знаменателе:
-2/√2 * √2/√2 = -2√2/2 = - √2
у₃ = 4 - √2;
у₄ = -2/-√2 + 4
Избавиться от иррациональности в знаменателе:
2/√2 * √2/√2 = 2√2/2 = √2
у₄ = 4 + √2.
Получили четыре пары решений данной системы уравнений:
(1; 2); (-1; 6); (√2; 4-√2); (-√2; 4+√2).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.