Помогите решить,пожалуйста,30 баллов

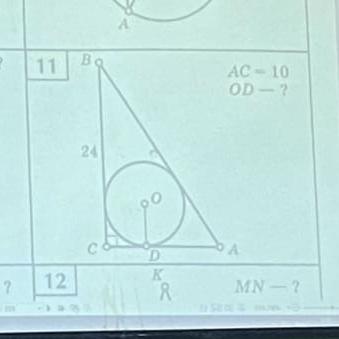
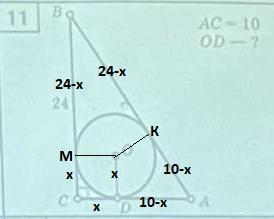
Свойство отрезков касательных для прямоугольного треугольника.

Объяснение:

ОD-радиус , проведенный в точку касания, значит ∠CDO=90°.

ОМ-радиус , проведенный в точку касания, значит ∠МОD=90°.

∠С=90° .Угол  ∠МОD=360-3*90°=90°⇒ четырехугольник СМОD-квадрат. Пусть ОD=ОМ=СD=СМ=х .

ОК-радиус , проведенный в точку касания, значит АВ=ВК+КА.

Тогда DA=10-x и по свойству отрезков касательных АК=10-х .

Тогда МВ=24-x и по свойству отрезков касательных ВК=24-х .

Гипотенуза АВ , с одной стороны равна 26(*) ,

                            с другой стороны (24-х)+(10-х).

Получаем уравнение   (24-х)+(10-х)=26  или х=4. Значит ОD=4/

===========================

(*) По т. Пифагора АВ=√(СВ²+СА²)=√(576+100)=√676=26