Алгебра, вопрос задал dumbface , 2 года назад

помогите решить плз
20 баллов ​

Приложения:

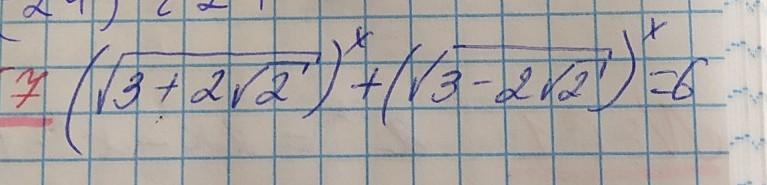
Ответы на вопрос

Ответил NNNLLL54
1

Ответ:

Числа  a  и   \dfrac{1}{a}   называются взаимно обратными ,   a\cdot \dfrac{1}{a}=1  .

Взаимно обратными числами являются и числа  \sqrt{3+2\sqrt2}  и  \sqrt{3-2\sqrt2}  .

Действительно,

 \sqrt{3-2\sqrt2}=\dfrac{\sqrt{3-2\sqrt2}\cdot \sqrt{3+2\sqrt2}}{\sqrt{3+2\sqrt2}}=\dfrac{\sqrt{9-4\cdot 2}}{\sqrt{3+2\sqrt2}}=\dfrac{1}{\sqrt{3+2\sqrt2}}    

Заменим в уравнении одно из чисел на обратное ему.

(\sqrt{3+2\sqrt2})^{x}+(\sqrt{3-2\sqrt2})^{x}=6\\\\(\sqrt{3+2\sqrt2})^{x}+\dfrac{1}{(\sqrt{3+2\sqrt2})^{x}}=6\\\\\\t=(\sqrt{3+2\sqrt2})^{x}>0\ \ ,\ \ \ t+\dfrac{1}{t}-6=0\ \ ,\ \ \ \dfrac{t^2-6t+1}{t}=0\ ,\ \ t\ne 0\\\\\\t^2-6t+1=0\ \ ,\ \ D/4=3^2-1=8\ \ ,\\\\t_1=3-\sqrt8=3-2\sqrt2\ \ ,\ \ \ t_2=3+2\sqrt2\\\\\\a)\ (\sqrt{3+2\sqrt2})^{x}=3-2\sqrt2\ \ ,\ \ (\sqrt{3+2\sqrt2})^{x}=\dfrac{1}{3+2\sqrt2}\ \ ,\\\\(3+2\sqrt2)^{\frac{x}{2}}=(3+2\sqrt2)^{-1}\ \ ,\ \ \ \dfrac{x}{2}=-1\ \ ,\ \ x=-2

b)\ \ (\sqrt{3+2\sqrt2})^{x}=3+2\sqrt2\ \ ,\ \ (3-2\sqrt2)^{\frac{x}{2}}=3+2\sqrt2\ \ ,\ \ \dfrac{x}{2}=1\\\\{}\ \ \ \ \ x=2\\\\Otvet:\ \ x_1=-2\ ,\ \ x_2=2\ .

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
Объясните как вы понимаете последней смысл пословицы учение-свет а не учение-тьма Серафима...
Английский язык, 1 год назад
помогите как сделать 4 задание там нужно ответеть из текста или что...
Биология, 2 года назад
... решите, прошу!!! ​
Русский язык, 2 года назад
Что не может быть выражено глаголом? А) Действие Б) Состояние В) Процесс Г) Признак ПОМОГИТЕ ПЖПЖПЖ​...
История, 8 лет назад
Как в архитектуре отразились взгляды человека на мир и себя? (в связи с темой "Памятники ренессансной архитектуры")...
Математика, 8 лет назад
В классе 15 мальчиков болеют за футбольную команду, 12 - за баскетбольную команду. Всего в классе 25 мальчиков. Сколько мальчиков болеют за обе команды, если все мальчики болеют хотя бы за одну...