Алгебра, вопрос задал Liudmilamila20 , 1 год назад

помогите решить определенные интегралы )

Приложения:

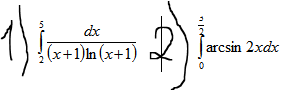
nafanya2014: вместо ? поставьте ту дробь, которая написана в верхнем пределе второго интеграла

Ответы на вопрос

Ответил nafanya2014

$\int\limits^5_2 { \frac{dx}{(x+1)ln(x+1)} } \, = \int\limits^5_2 { \frac{d(ln(x+1)}{ln(x+1)} } \, =ln(ln(x+1) ^{5}_{2} =lnln6-lnln3=ln \frac{ln6}{ln3}$

$\int\limits^{?}_0 {arcsin2x} \, dx=$
интеграл считают по частям
u=arcsin2x du=(arcsin2x)`dx=1/√(1-4х²) ·(2х)`dx=2dx/√(1-4x²)
dv=dx v= x

$=xarcsinx^{?}_0- \int\limits^{?}_0 { \frac{2x}{ \sqrt{1-4 x^{2} } } } \, dx = \\ =?arcsin{?}-0+ \frac{1}{4} \int\limits^{?}_0 { \frac{d(1-4 x^{2} )}{ \sqrt{1-4 x^{2} } } } \, dx = \\ =?arcsin{?}+ \frac{1}{4}\cdot 2 \sqrt{1-4 x^{2} }^{?}_0= \\ = ?arcsin{?}+ \frac{1}{2}\cdot \sqrt{1-4 (?)^{2} }^{?}- \frac{1}{2}\cdot \sqrt{1-4 (0)^{2} }= \\ = ?arcsin{?}+ \frac{1}{2}\cdot \sqrt{1-4 (?)^{2} }^{?}- \frac{1}{2}\cdot \sqrt{1 }$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Напишите пожалуйста как читать русскими буквам:Yes-ес...

Русский язык, 1 год назад

Раскройте скобки , вставьте пропущенные буквы и расставьте знаки препинания: I.1.Поезд мчал его на юг к морю ув_зя от сырой д_ждливой ос_ни к тёплым берегам Южного Крыма. 2.Вечером после ужина мы...

Другие предметы, 1 год назад

помогите сочинить стих со словом абориген...

Русский язык, 1 год назад

Объяснить старинную поговорку. Кострома городок - Москвы уголок...

Литература, 7 лет назад

с каким событием в жизни Пушкина связано стихотворение "И. И. Пущину"...

Математика, 7 лет назад

Сколько будет 14/25 + 3/8...