Алгебра, вопрос задал Phedwassmin , 6 лет назад

Помогите решить логарифмическое уравнение №3

Приложения:

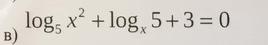
ninjazahar056: а нужно упростить?

Ответы на вопрос

Ответил Universalka

1

$\displaystyle\bf\\ODZ:\\x>0 \ \ , \ \ x\neq 1\\\\\\\log_{5}x^{2} +\log_{x} 5+3=0\\\\2\log_{5} x+\frac{1}{\log_{5}x }+3=0\\\\\\\log_{5} x=m\\\\\\2m+\frac{1}{m} +3=0\\\\\\\frac{2m^{2} +3m+1}{m} =0\\\\\\2m^{2} +3m+1=0\\\\\\D=3^{2}-4\cdot2\cdot 1=9-8=1\\\\\\m_{1} =\frac{-3-1}{4} =-1\\\\\\m_{2} =\frac{-3+1}{4} =-\frac{1}{2}$

$\dsisplaystyle\bf\\1)\\\\\log_{5} x=-1\\\\\\x_{1} =5^{-1} =\frac{1}{5} =0,2\\\\\\2)\\\\\log_{5} x=-\frac{1}{2} \\\\\\x_{2} =5^{-\frac{1}{2} } =\frac{1}{\sqrt{5} } =\frac{\sqrt{5} }{5} \\\\\\Otvet:0,2 \ \ ; \ \ \frac{\sqrt{5} }{5}$

Ответил ZlataSergeeva2000

1

Решение:

$log_5~x^2 + log_x5 + 3 = 0$

ОДЗ: x > 0

$log_x5 = \dfrac{1}{log_5~x}$

$2log_5~x + \dfrac{1}{log_5~x} + 3 = 0$

$2(log_5~x)^2 + 3log_5~x + 1 = 0$

Замена

$log_5~x = t$

2t² + 3t + 1 = 0

D = 3² - 4 · 1 · 2 = 1

t₁ = 0.25 · (-3 -1) = -1

t₂ = 0.25 · (-3 +1) = -0.5

Возвращаемся к замене

$log_5~x = -1;~~~~~~x_1 = \dfrac{1}{5} = 0.2 ;$

$log_5~x = -0.5;~~~~~x_2 = \dfrac{1}{\sqrt{5} } = \dfrac{\sqrt{5} }{5} = 0.2\sqrt{5} ~;$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Сочинение на тему "my best holiday" мои лучшие каникулы (на английском)...

Русский язык, 1 год назад

какие звуки повторяются в скороговорке на дворе трава на траве дрова...

История, 6 лет назад

какое значение имела колонизация дикого поля в экономической жизни украинских земель...

Қазақ тiлi, 6 лет назад

61бет 7тапсырма 5-сынып...

Биология, 8 лет назад

поясните значение знаков мужская гамета и женская плиз)))(((((((((((((...

Математика, 8 лет назад

Помогите срочно решить !!! Заранее спасибо...