Помогите решить логарифм
Приложения:
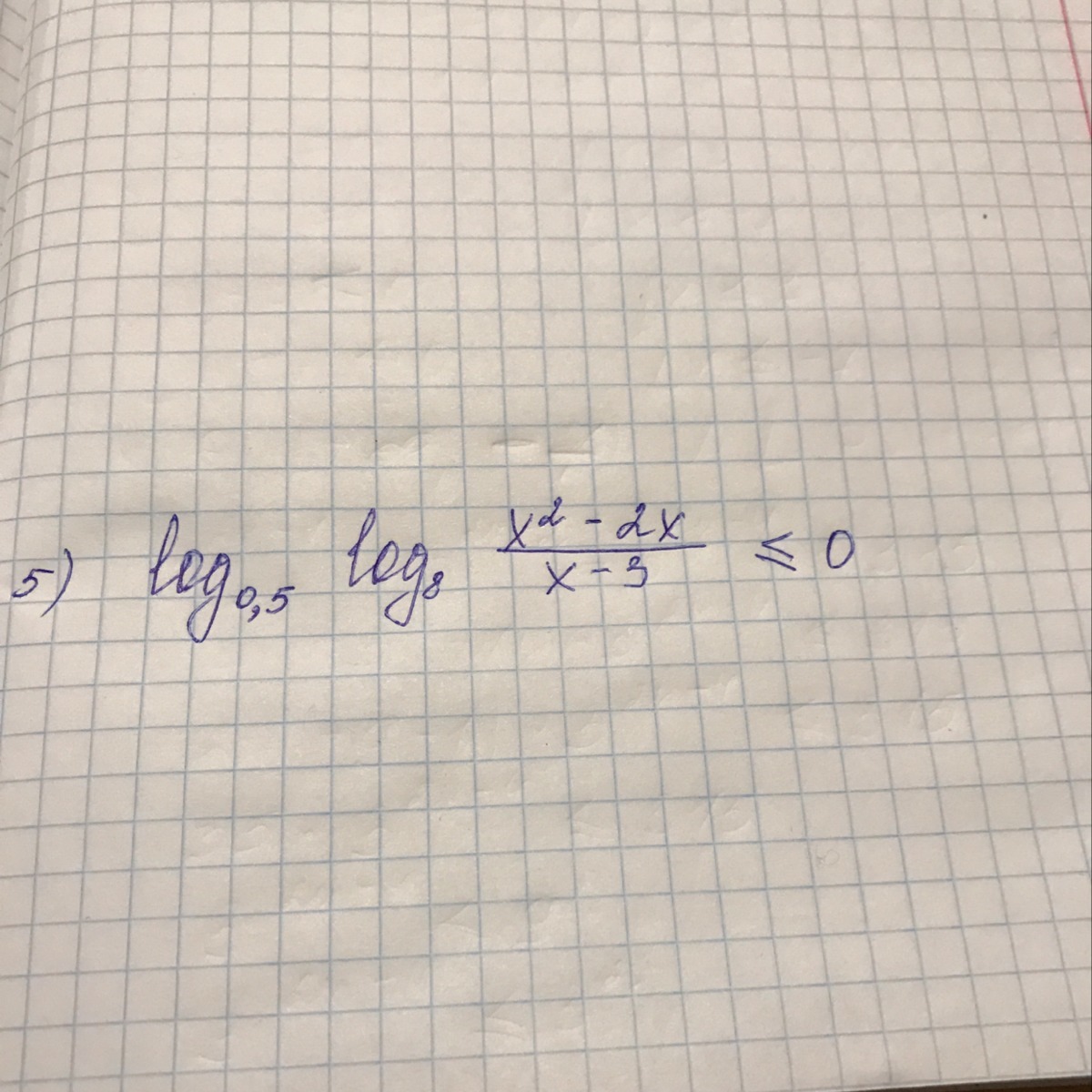
Ответы на вопрос
Ответил zanykmarkooyjp1p
0
log0.5(log8(x²-2x/x-3))≤0
x ∈ (3;+∞)
log8(x²-2x/x-3)≥0.5^0
log8(x²-2x/x-3)≥1
x²-2x/x-3≥8
x²-2x/x-3-8≥0
x²-2x-8+24/x-3≥0
x²-10x+24/x-3≥0
x²-4x-6x+24/x-3≥0
x×(x-4)-6(x-4)/x-3≥0
(x-6)×(x-4)/x-3≥0
система { (x-6)×(x-4)≥0 система { x ∈ (-∞;4] ∪ [6;+∞)
x-3>0 x>3
система { (x-6)×(x-4)≤0 система { x ∈ [4;6]
x-3<0 x<3
x ∈ (3;4] ∪ [6;+∞)
x ∈ ∅
x ∈ (3;4] ∪ [6;+∞), x ∈ (3;+∞)
Ответ: x ∈ (3;4] ∪ [6;+∞).
там система из двох уравнений; етот знак / означает деление
x ∈ (3;+∞)
log8(x²-2x/x-3)≥0.5^0
log8(x²-2x/x-3)≥1
x²-2x/x-3≥8
x²-2x/x-3-8≥0
x²-2x-8+24/x-3≥0
x²-10x+24/x-3≥0
x²-4x-6x+24/x-3≥0
x×(x-4)-6(x-4)/x-3≥0
(x-6)×(x-4)/x-3≥0
система { (x-6)×(x-4)≥0 система { x ∈ (-∞;4] ∪ [6;+∞)
x-3>0 x>3
система { (x-6)×(x-4)≤0 система { x ∈ [4;6]
x-3<0 x<3
x ∈ (3;4] ∪ [6;+∞)
x ∈ ∅
x ∈ (3;4] ∪ [6;+∞), x ∈ (3;+∞)
Ответ: x ∈ (3;4] ∪ [6;+∞).
там система из двох уравнений; етот знак / означает деление
Новые вопросы