Математика, вопрос задал milakamilat1m , 6 лет назад

Помогите решить интегрирование тригонометрической функции, пример: $\int\limits {tg^5x} \, dx$ . Ответ должен получится: $\frac{1}{4} tg^4x - \frac{1}{2} tg^2x-ln|cosx|+C$

Ответы на вопрос

Ответил LymarIvan

1

Ответ:

Пошаговое объяснение:

$\int {\rm tg^5x} \, dx =\begin{Vmatrix}t=\rm tg \; x\\x=\rm arctg \; t\\dx=\frac{dt}{1+t^2} \end{Vmatrix}=\int {t^5*} \, \frac{dt}{1+t^2} =\int {(t^3-t+\frac{t}{1+t^2} )} \, dt =\\\int {(t^3-t)} \, dt+\frac{1}{2}\int {\frac{2t}{1+t^2} } \, dt =\int {(t^3-t)} \, dt+\frac{1}{2}\int {\frac{d(1+t^2)}{1+t^2} } \, =\\\frac{t^4}{4}-\frac{t^2}{2}+\frac{1}{2}\ln| 1+t^2| +C=\frac{1}{4}\rm tg^4x -\frac{1}{2}\rm tg^2x+\frac{1}{2} \ln| 1+\rm tg^2x|+C=$

$\frac{1}{4}\rm tg^4x -\frac{1}{2}\rm tg^2x+\frac{1}{2} \ln|\cos^{-2}x|+C=\frac{1}{4}\rm tg^4x -\frac{1}{2}\rm tg^2x- \ln|\cos x|+C=$

В конце воспользовался свойством логарифма

$\log_a{b^n }=n\log_a{b}$

Приложения:

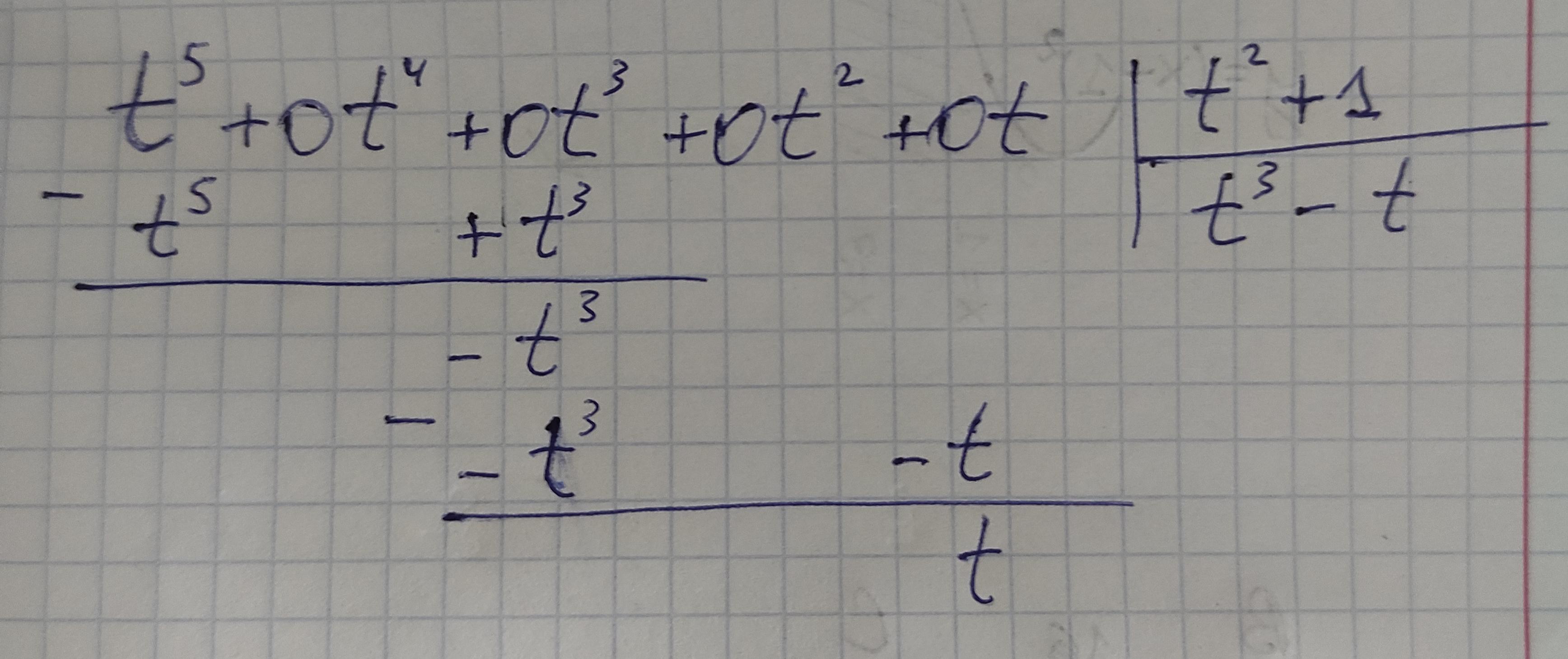
milakamilat1m: Спасибо большое, а знаешь как решить первый мой вопрос за сегодня ?

LymarIvan: там формула поломалась

LymarIvan: не могу разобрать условие

milakamilat1m: добавила снова

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

как перевести 3км\ч в метры и минуты...

История, 1 год назад

ответ в кратко! Почему имя Спартака даже спустя 2 тыс. лет после его восстания такое известное и уважаемое?

Алгебра, 6 лет назад

помогите пожалуйста...

Русский язык, 6 лет назад

5,6. Укажите лишнее слово в синонимическом ряду а) робеть б) бранить в) опасаться г) трусить 7. Не является антонимом к существительному «давать» а) брать б) отбирать в) предлагать г)...

Математика, 8 лет назад

Знайти похидну функции : у= 1÷√7...

Математика, 8 лет назад

ПОМОГИТЕ РЕШИТЬ 770 УПР 5 КЛАСС...