помогите решить хотя бы одно задание !!! пожалуйста
тема: корінь n- го степеня
Приложения:
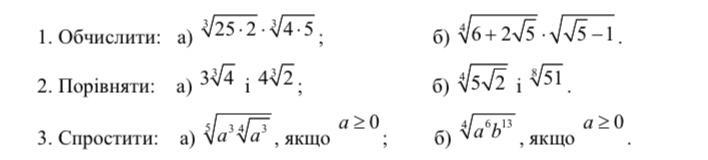
Ответы на вопрос
Ответил sangers1959
2
Объяснение:
1.
2.
3.
Jdhfjdjc:
спасибо огромное!!
Новые вопросы
Русский язык,
1 год назад
Окружающий мир,
6 лет назад
Математика,
6 лет назад
Математика,
8 лет назад
Физика,
8 лет назад