Геометрия, вопрос задал daradinah , 6 лет назад

помогите решить, даю 35 баллов

Приложения:

Ответы на вопрос

Ответил settom

Ответ:

$a_{3}= 12\\S_{3} =36\sqrt{3} \\\\P_{4} =8\sqrt{6} \\\\S_{4} =24$

Объяснение:

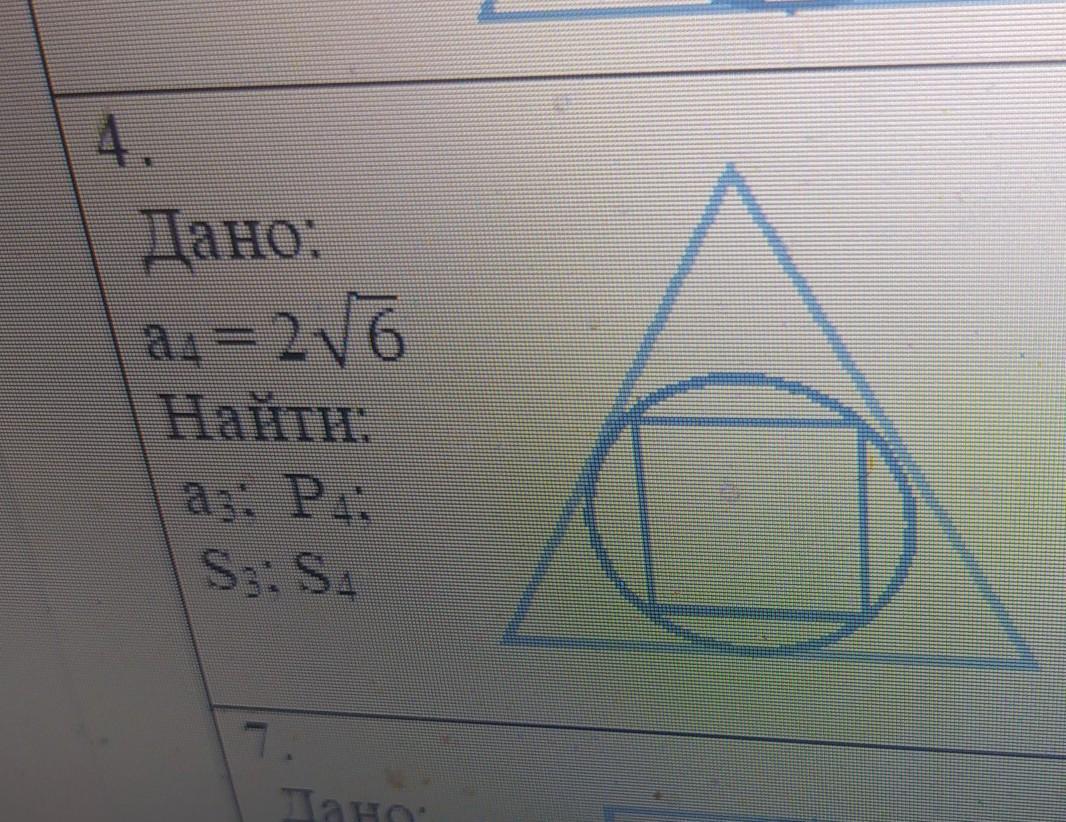
Если a4 - это сторона квадрата (что из условия не ясно), но перимерт квадрата равен

$P_{4}=4*2\sqrt{6}=8\sqrt{6} \\$

Площадь квадрата

$S_{4} =2\sqrt{6}* 2\sqrt{6}=24$

Радиус описанной окружности будет равен половине диагонали

$r=\frac{1}{2}\sqrt{(2\sqrt{6} )^{2} +2\sqrt{6} )^{2} } = \frac{1}{2}\sqrt{24+24 }=\frac{1}{2}\sqrt{48 }=\frac{4\sqrt{3}}{2}=2\sqrt{3}$

радиус вписанной в правильный треугольник окружности

$r=\frac{a}{2\sqrt{3} }$

то есть сторона треугольника будет

$a_{3} =r*2*\sqrt{3} = 2*\sqrt{3}*2*\sqrt{3} = 12$

Высота треугольника

$h=\sqrt{12^{2}-6^{2} } =\sqrt{144-36} =\sqrt{108} =6\sqrt{3}$

Площадь треугольника

$S_{3} =\frac{1}{2} *12*6\sqrt{3} =36\sqrt{3}$

Новые вопросы

Биология, 1 год назад

Литература, 1 год назад

География, 6 лет назад

География, 6 лет назад

Математика, 8 лет назад

Математика, 8 лет назад