Математика, вопрос задал luter2020 , 6 лет назад

Помогите решить. Числа в колонках это варианты ответов. Нужно решение. Даю 100 балов

Приложения:

Ответы на вопрос

Ответил pushpull

1

Ответ:

Пошаговое объяснение:

1.

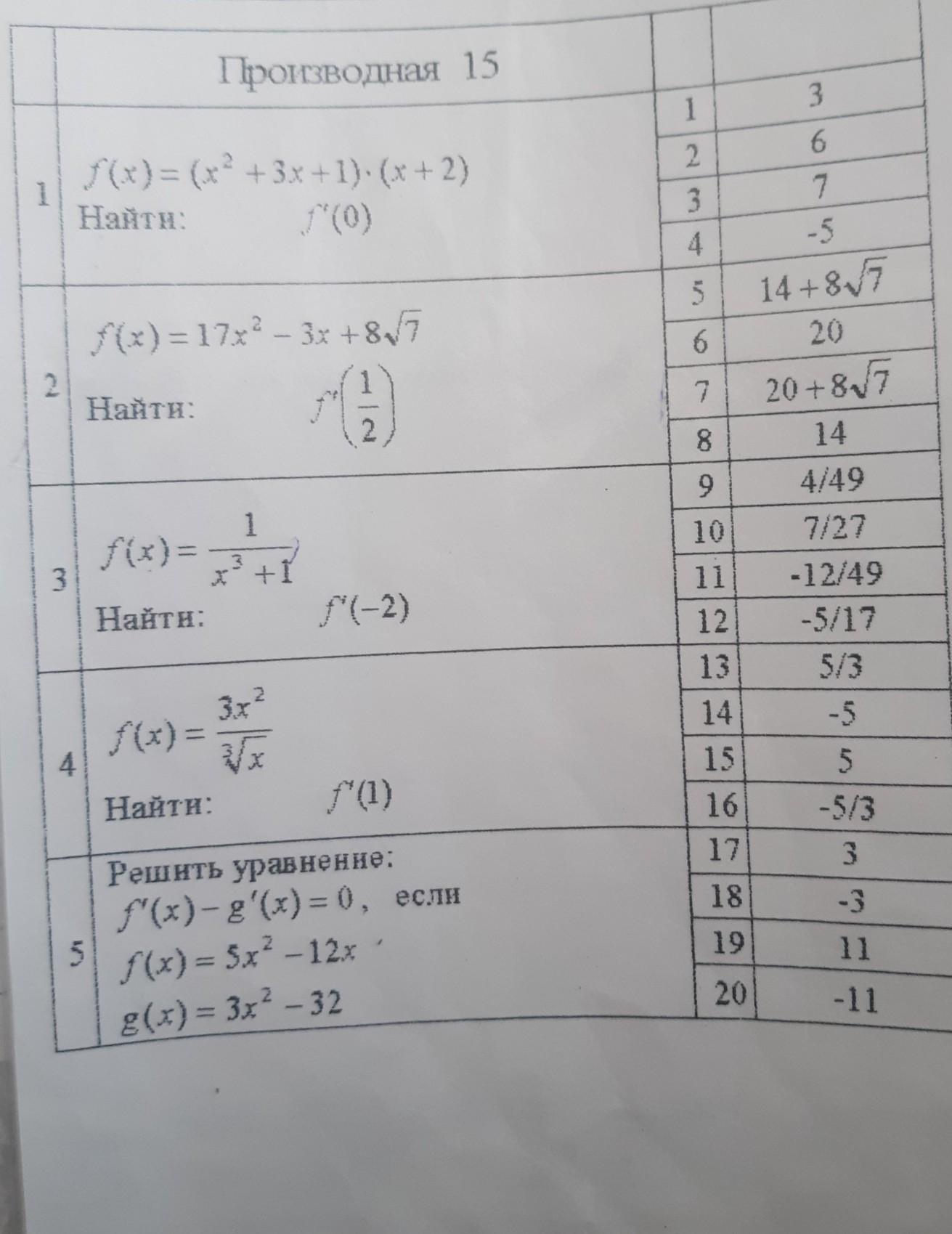
$\displaystyle (uv)' = u'v +uv'\\f'(x)=\bigg ((x^2+3x+1)(x+2)\bigg )' = (x^2+3x+1)'(x+2)+(x^2+3x+1)(x+2)'=\\=(2x+3)(x+2)+((x^2+3x+1)*1\\\\f'(0) = 3*2+1=7$

ответ №3 f'(0)=7

2.

$\displaystyle f'(x) = (17x^2-3x+8\sqrt{7} )'=17*2x-3=34x-3\\\\f'(0.5) = 34*0.5-3 = 17-3 = 14$

ответ № 8 f'(0.5) = 14

3.

$\displaystyle \bigg(\frac{1}{u}\bigg )' =-\frac{1}{u^2}\\\\(f(g(x))' = f'(g)*g'(x)\\\\f'(x) = \bigg(\frac{1}{x^3+1} \bigg)'=-\frac{1}{(x^3+1)^2} *3x^2\\\\f'(-2) = -\frac{1}{((-2)^2+1)^2} *3*4=-\frac{12}{49}$

ответ №11 f/(-2) = -12/49

4.

$\displaystyle (x^n)'=nx^{n-1}\\\\\bigg (\frac{3x^2}{\sqrt[3]{x} } \bigg )'=(3x^{5/3})'=3*\frac{5}{3} x^{5/3 -1}=5x^{2/3}\\\\f'(1) = 5$

ответ № 15 f'(1) = 5

5.

$\displaystyle f'(x)'=(5x^2-12x)' = 10x-12\\\\g'(x) = (3x^2-32)'=6x\\\\f'(x)-g'(x) = 10x-12-6x\\10x-12-6x=0\\4x=12\\\\\boldsymbol {x=3}$

ответ №17 х=3

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Раскройте скобки употребив глаголы в нужном времени (Present Indefinite/Present Continuous) 1. He ( to study) at the Maritime College. 2. They (to learn) some new rules every evening. 3. Now...

Алгебра, 1 год назад

СРОЧНО 80БАЛЛОВ!!!! Вычислите площадь фигуры, ограниченой : $y=- x^{2} +3; y=2x$ ...

Обществознание, 6 лет назад

Образцы заданий и схемы выставления баллов Задания суммативного оценивания за 1 четверть по предмету «Русская литература» Понимание и ответы по тексту Задания 1. Ответьте на вопросы, выбрав...

Алгебра, 6 лет назад

Помогите решить -2,6 < 5x-2<3...

Математика, 8 лет назад

Одна из трёх данных последовательностей составлена по это правилу а)2, 6, 18, ... б)2, 6, 10, ... в)2, 6, 14, ...

Литература, 8 лет назад

отношение Осипа и Городничего к Хлестакову?