Помогите решить. Алгебра 11 класс.
Приложения:



Simba2017:
производные прошли?
да
Ответы на вопрос
Ответил Simba2017
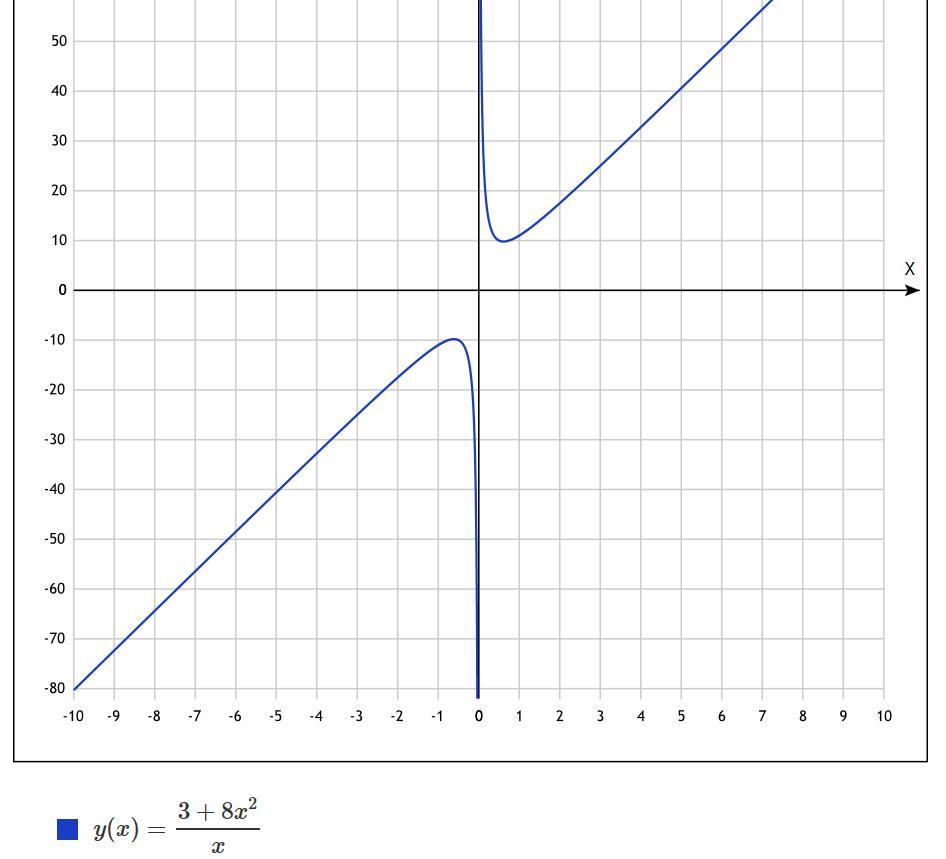
1
ОДЗ: x≠0
f`(x)=0
f`(x)=(16x^2-3-8x^2)/x^2=(8x^2-3)/x^2=0
8x^2=3
x^2=3/8
x=-√(3/8) и √(3/8)-экстремальные точки
посмотрим как ведет себя производная на интервалах
+++(-√3/8))----(0)----(√(3/8))+++
f(-√(3/8)=6/(-√(3/8))-максимум
f(√3/8)=6/(√(3/8))-минимум
Ответ f(x) растет на интервалах х= (-∞;-√(3/8))U(√(3/8);+∞) и убывает на
x=(-√(3/8);0)U(0;√(3/8)
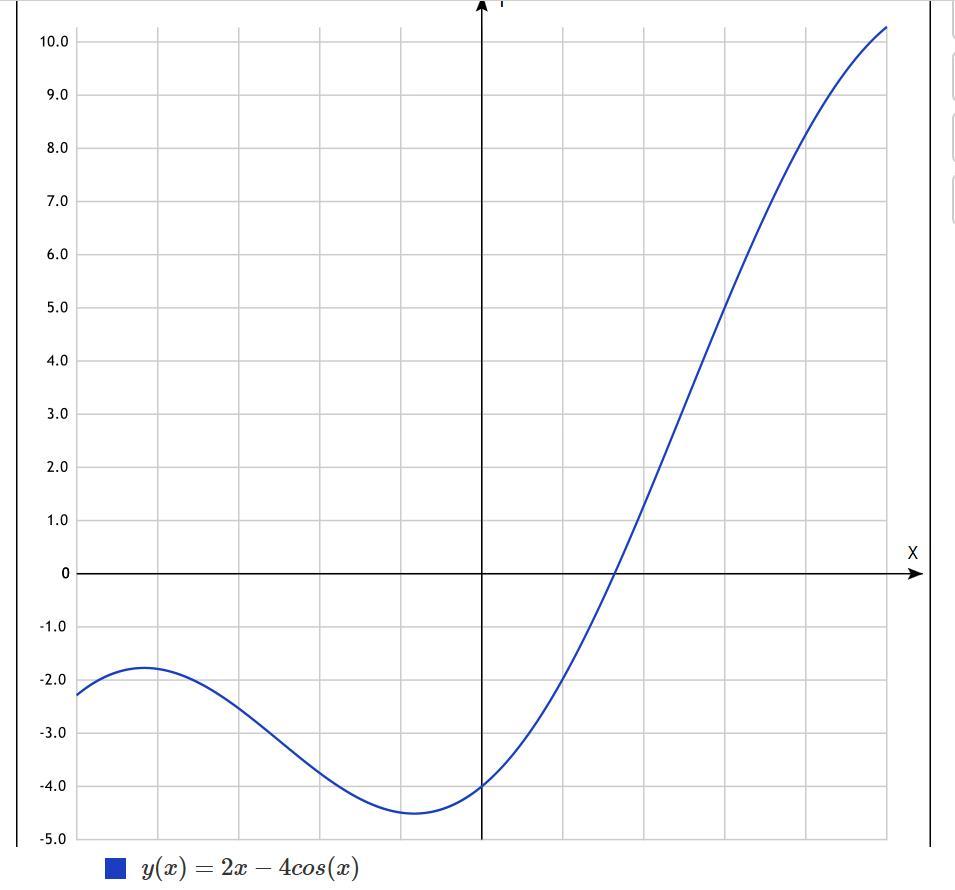
2)y`(x)=2+4sinx
4sinx=-2; sinx=-1/2; x=-pi/6+2pik и x=-5pi/6+2pik
в указанный интервал вошла одна точка x=-pi/6
y(-pi/6)=2*(-pi/6)-4*cos(-pi/6)=-pi/3-2√3≈-4.5
посмотрим знаки производной на этом интервале
----(-pi/6)+++
x=-pi/6-точка минимума, в градусах это -180/6=-30 градусов
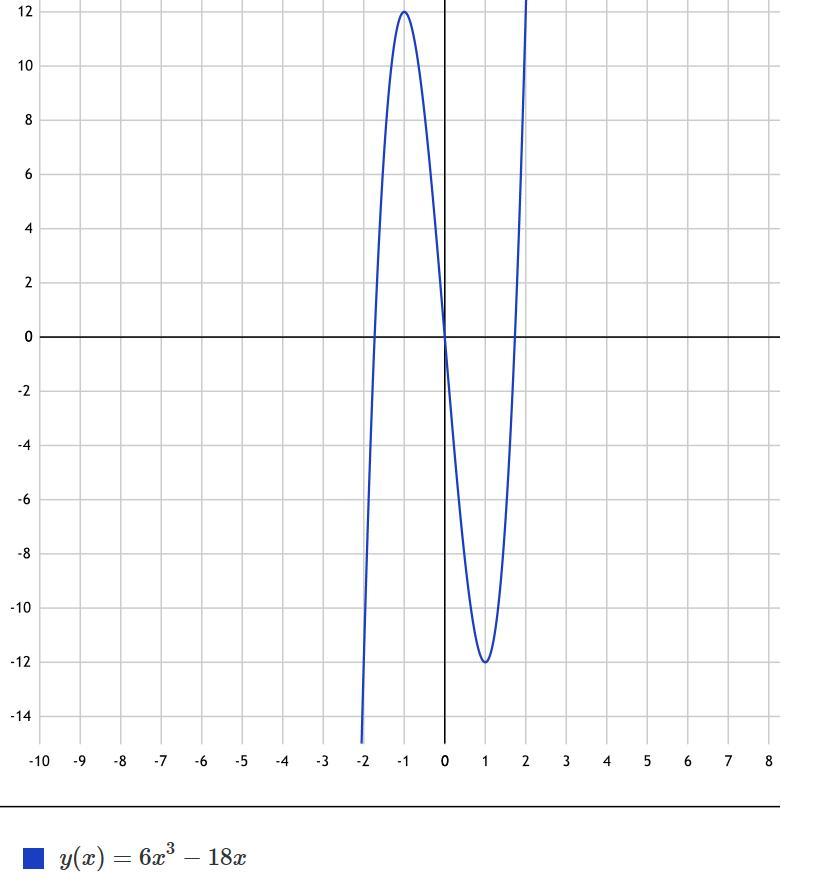
3) y`=18x^2-18
18(x^2-1)=0 x=+-1
y(1)=6-18=-12-минимум
y(-1)=-6+18=12-максимум
у убывает на x=(-1;1)
тогда с+8≥-1; c+10≤1
с≥-9; c≤-9
Ответ c=-9
Приложения:
Новые вопросы
Математика,
1 год назад
Английский язык,
1 год назад
Английский язык,
1 год назад
Геометрия,
1 год назад
Русский язык,
6 лет назад