Алгебра, вопрос задал HotPukan , 7 лет назад

Помогите решить!
а) Решите уравнение (10 cos^2 + cosx - 2) / (√-sinx) = 0
б) Найдите все корни этого уравнения, принадлежащие промежутку ( -π ; 3π/2)

Ответы на вопрос

Ответил NeZeRAvix

$tt dfrac{10cos^2x+cosx-2}{sqrt{-sinx}} =0$

ОДЗ:

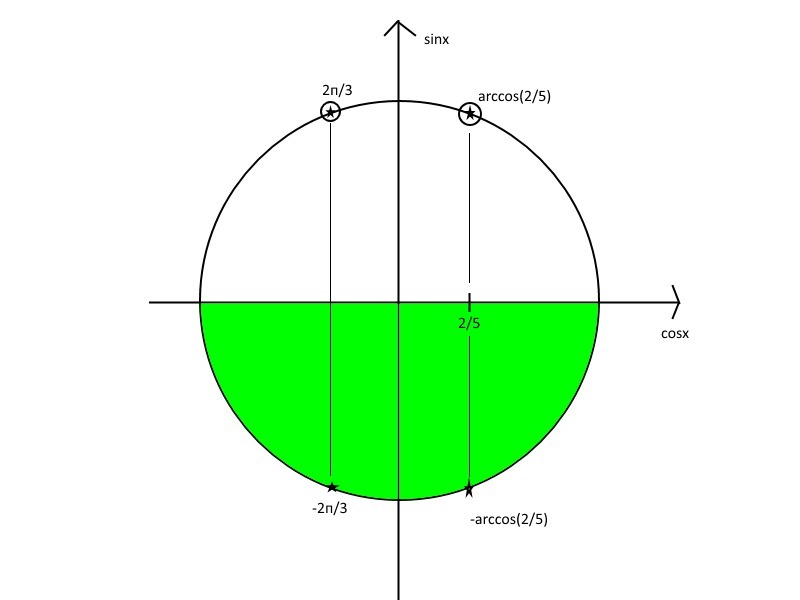
-sinx>0 ⇒ sinx<0 ⇒ x ∈ III, IV координатным четвертям (не включая концы).

$tt 10cos^2x+cosx-2=0\ D=1+80=81=9^2\ cosx_1=dfrac{-1-9}{20}=-dfrac{1}{2} Rightarrow x=pmdfrac{2 pi}{3}+2pi k\ cosx_2=dfrac{-1+9}{20}=dfrac{2}{5} Rightarrow x =pm arccos dfrac{2}{5}+ 2 pi k$

Теперь отбираем корни по ОДЗ (первая картинка). Остаются две серии корней.

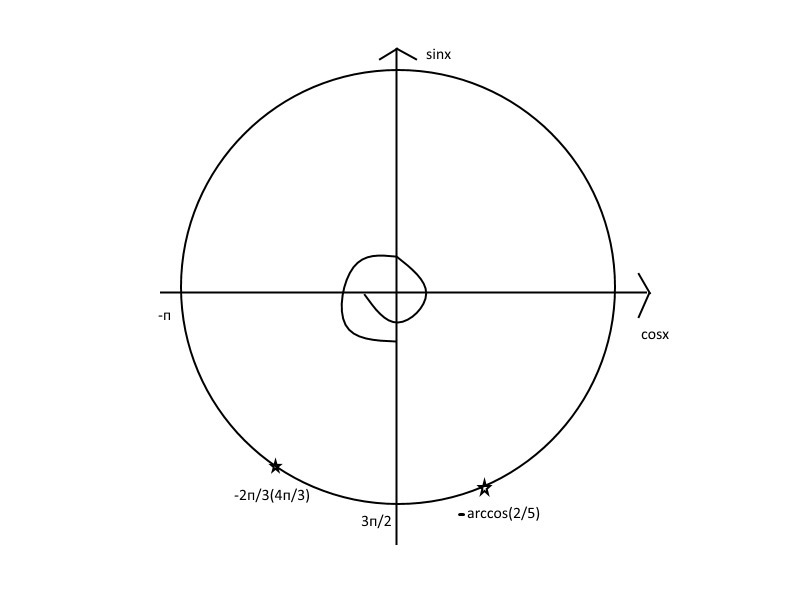
$tt x=left[begin{array}{I}tt -dfrac{2 pi}{3}+2 pi k \ tt -arccosdfrac{2}{5}+2 pi k end{array}} ; k in Z$

И напоследок отбор корней на промежутке (вторая картинка).

Ответ: а) $tt x=left[begin{array}{I}tt -dfrac{2 pi}{3}+2 pi k \tt -arccosdfrac{2}{5}+ 2 pi k end{array}}; k in Z$ , б) $tt -dfrac{2 pi }{3}, dfrac{4 pi}{3}, -arccosdfrac{2}{5}$