Алгебра, вопрос задал balndin1204 , 2 года назад

помогите решить 5 задание

Приложения:

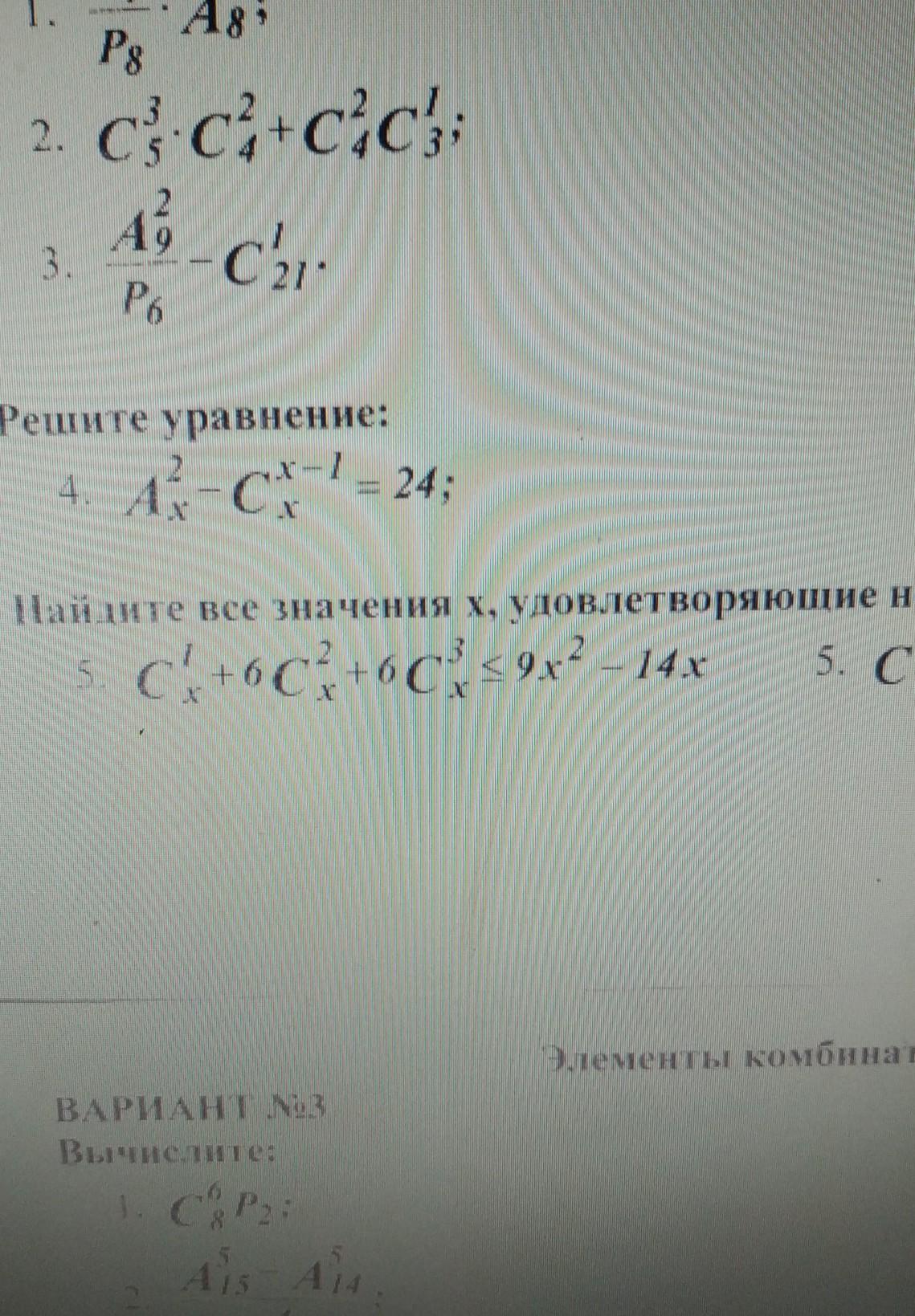
Ответы на вопрос

Ответил sangers1959

0

Объяснение:

ОДЗ:

$x\in\mathbb N,\ \ \ \ x\geq 3.$

$C_x^1+6*C_x^2+6*C_x^3\leq 9x^2-14x\\\frac{x!}{(x-1)!*1!}+\frac{6*x!}{(x-2)!*2!} +\frac{6*x!}{(x-3)!*3!} \leq 9x^2-14x\\\frac{(x-1)!*x}{(x-1)!*1}+\frac{6*(x-2)!*(x-1)*x}{(x-2)!*1*2} +\frac{6*(x-3)!*(x-2)*(x-1)*x}{(x-3)!*1*2*3} \leq 9x^2-14x\\x+3*(x-1)*x+(x-2)*(x-1)*x\leq 9x^2-14x\\x+x*(3x-3)+x*(x^2-3x+2)-9x^2+14x\leq 0\\x*(1+3x-3+x^2-3x+2-9x+14)\leq 0\\x*(x^2-9x+14)\leq 0\\x*(x^2-7x-2x+14)\leq 0\\x*(x*(x-7)-2*(x-7))\leq 0\\x*(x-7)*(x-2)\leq 0$

-∞__-__0__+__2__-__7__+__+∞ ⇒

x∈(-∞;0]U[2;7].

Согласно ОДЗ:

Ответ: x=3, 4, 5. 6, 7.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

Кызыл ала кара кок сары ала кок ала создерине сойлем курау керек!

Другие предметы, 1 год назад

Напишите свою версию как вы думаете почему вымерли динозавры 10-15 предложений ПОЖАЛУЙСТА ПОМОГИТЕ НИ ЧЕГО ПРИДУМАТЬ НЕ МОГУ...

ОБЖ, 2 года назад

Губительнее всего алкоголь воздействует на: а) Опорно-двигательный аппарат; б) Сердце и кровеносные сосуды; в) Клетки головного мозга...

Алгебра, 2 года назад

ПОМОГИТЕ СРОЧНОО!! ПОЖАЛУЙСТА!!!!!!!!! при якому значенні змінної не має змісту вираз x2/4x-4...

Информатика, 7 лет назад

ввести с клавиатуры массив из 15 четных чисел...

Алгебра, 7 лет назад

найдите последнюю цифру числа которое является значением выражения 2 умножить на 351 в 17 степени плюс 3 умножить на 125 в 9 степени минус 106 в 7 степени...