помогите решить........
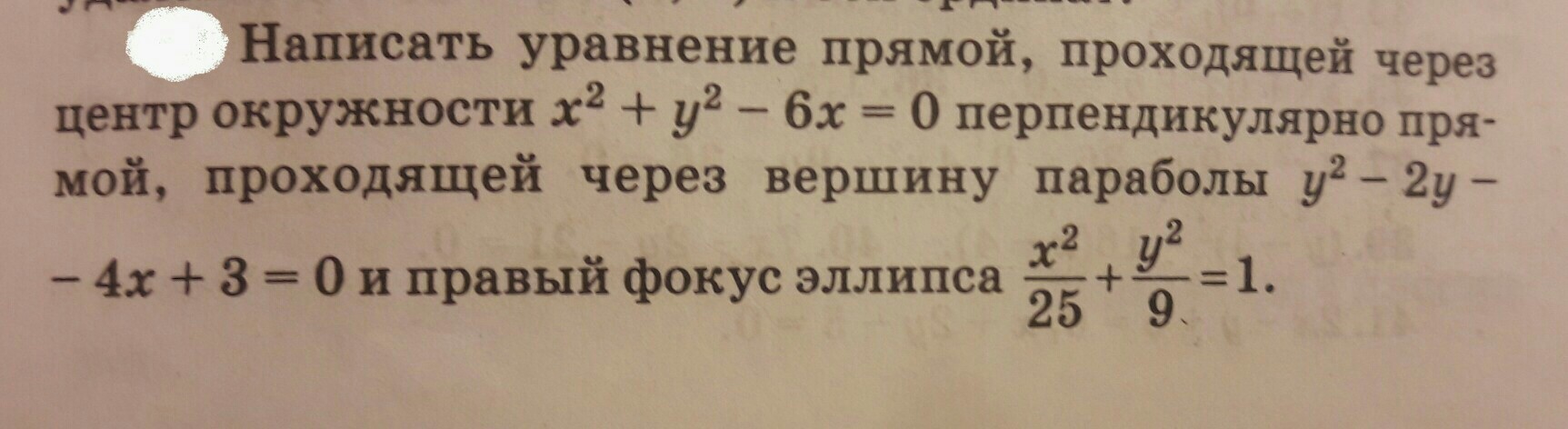
Ответы на вопрос
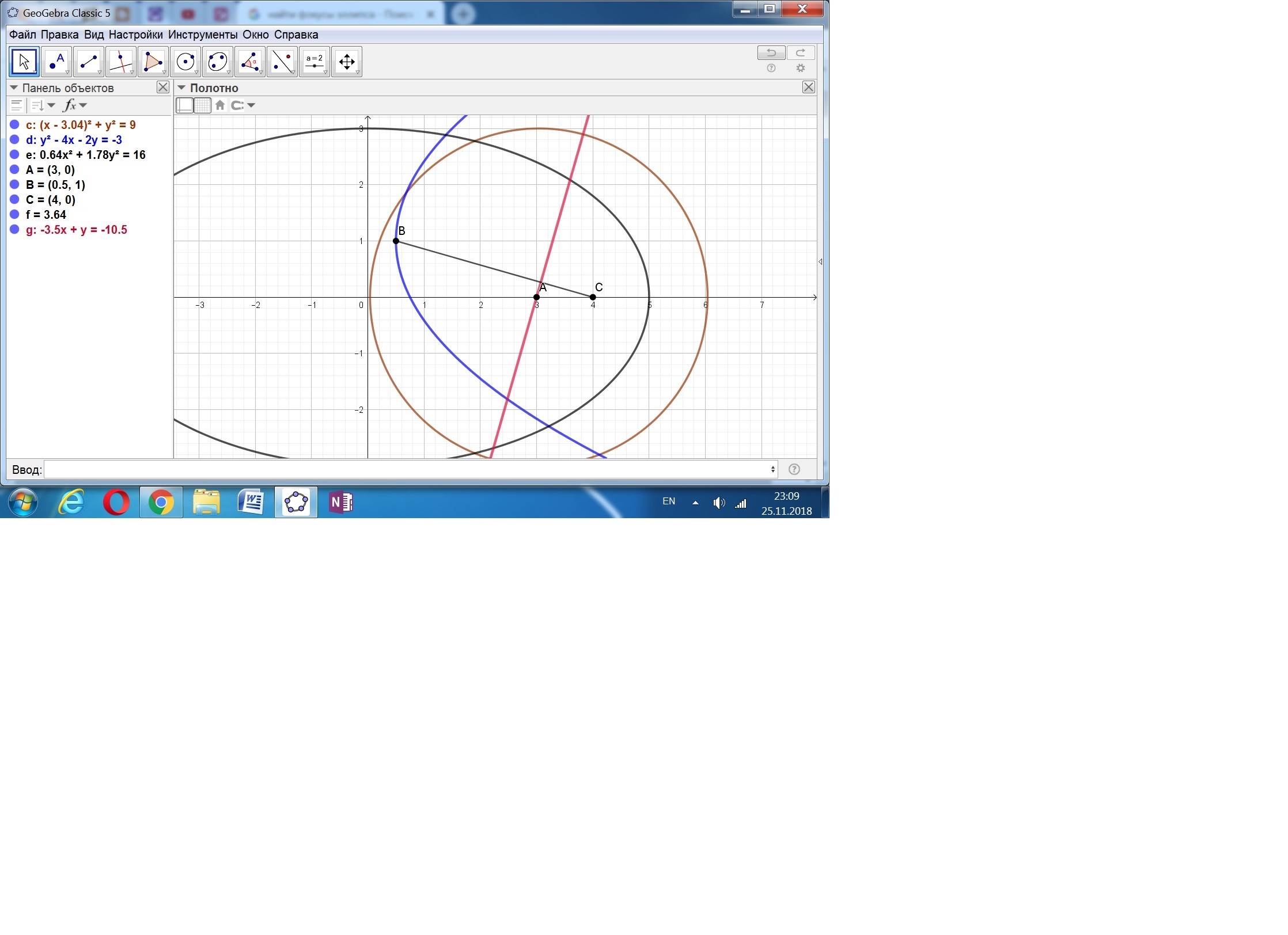
Уравнение окружности преобразуем с выделением полного квадрата.
(х² - 6х + 9) + у² - 9 = 0.
Получаем уравнение (х - 3)² + у² = 3².
Центр окружности (пусть это точка А): (3; 0).
Уравнение параболы приведём к каноническому виду.
(у² - 2у + 1)- 1 = 4х - 3,
(у - 1)² = 4(х - (1/2)). Вершина параболы (точка В): ((1/2); 1).
В уравнении эллипса по заданию а = 5, в = 3.
Находим с = √(а² - в²) = √25 - 9) = √16 = 4.
Так как эллипс с центром в начале координат, то координата првого фокуса (точка С): (4; 0).
Уравнение прямой ВС: (х - 4)/3,5 = у/-1.
Из канонической формы переведём в уравнение с угловым коэффициентом: -х + 4 = 3,5у. у = (-2/7)х + (8/7).
Угловой коэффициент искомого перпендикуляра к прямой АВ равен:
к = -1/к(АВ) = -1/(-2/7) = (7/2).
Уравнение имеет вид у = (7/2)х + в. Для определения параметра в подставим координаты точки А: 0 = (7/2)*3 + в.
Тогда в = -21/2.
Ответ: уравнение перпендикуляра у = (7/2)х - (21/2).