Помогите решить 3 вопрос.Пж
Приложения:
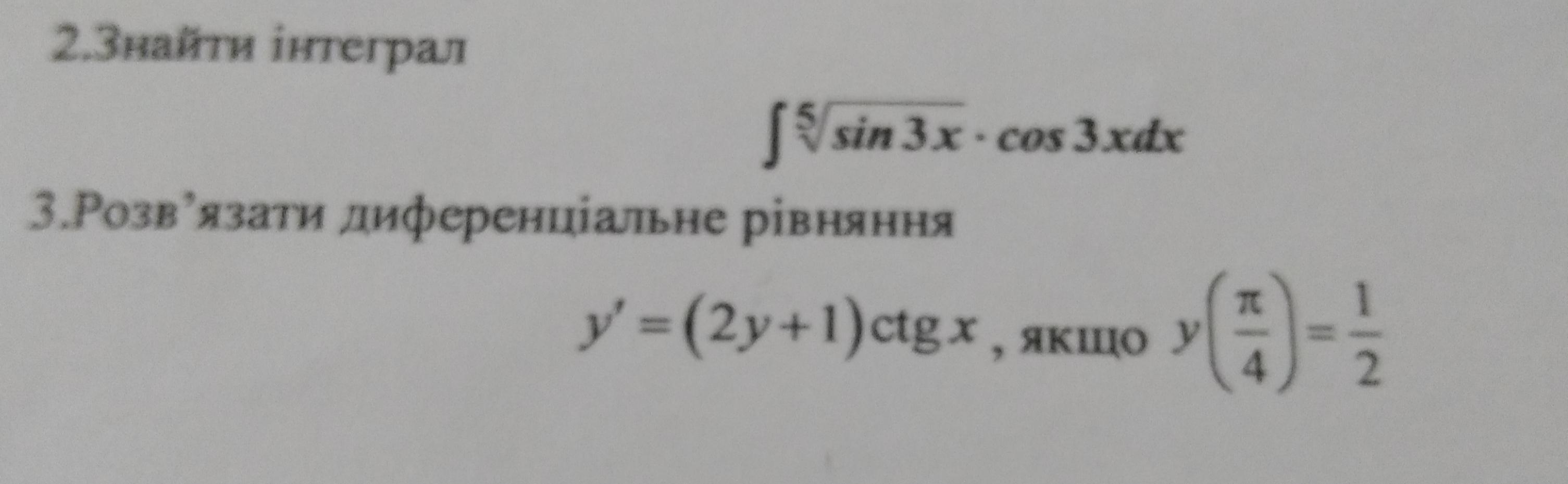
Ответы на вопрос
Ответил MatemaT123
1
Ответ:
Пошаговое объяснение:
Разделяем переменные:
Берём интегралы от обеих частей уравнения:
Подставляем значения из условия:
Подставляем значение константы:
Ответил dobra888
0
Ответ: у = 2sin²х - 0,5 .
Пошаговое объяснение:
dy/dx = ( 2y + 1 ) * cosx/sinx ; y ( π/4 ) = 1/2 ;
dy/( 2y + 1 ) = cosxdx / sinx ;
1/2 * dy/( y + 0,5 ) = d(sinx )/sinx ;
dy/( y + 0,5 ) = 2d(sinx )/sinx ; інтегруємо :
∫ dy/( y + 0,5 ) = ∫ 2d(sinx )/sinx ;
ln| y + 0,5 | = 2 ln| sinx | + ln| C | ;
ln| y + 0,5 | = ln| C || sinx |² ;
y + 0,5 = Csin²x ;
y = Csin²x - 0,5 ; - загальний розв"язок диф. рівняння
y ( π/4 ) = 1/2= С (sinπ/4)² - 0,5 ;
С (sinπ/4)²= 1 ;
C * (1 /√2 )² = 1 ;
C * 1/2 = 1 ;
C = 2 ; отже , у = 2sin²х - 0,5 - шуканий частинний розв"язок .
Новые вопросы