Помогите решить: 1) (1-ctg^2a+ctg^4a)/sin^2a = 1+ctg^6a; 2) 1/(1+ctga*ctg^2a) = 2sin^2a
Приложения:

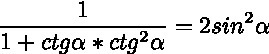
Ответы на вопрос
Ответил mishka19
0
1) правая часть:

левая часть:

левая часть равна правой части тождества => тождество верно
2) левая часть:

правая часть:

левая часть равна правой части тождества => тождество верно
левая часть:
левая часть равна правой части тождества => тождество верно
2) левая часть:
правая часть:
левая часть равна правой части тождества => тождество верно
Новые вопросы