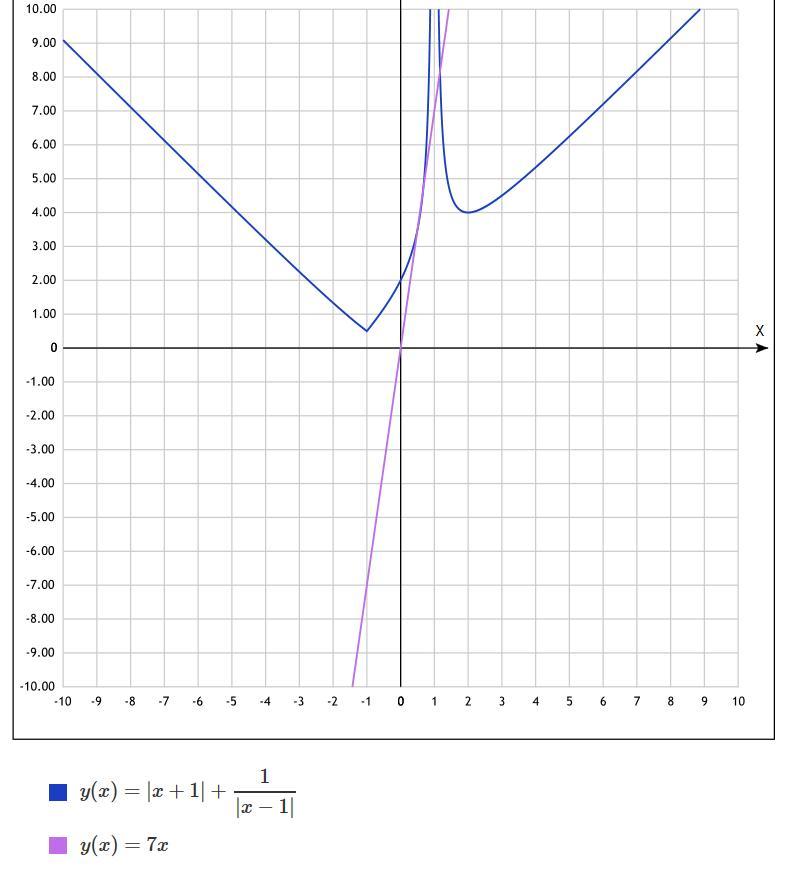
Помогите разобраться с модулем
|x+1|+1/|x-1|>7x
Ответы на вопрос
ОДЗ x≠1
найду точки пересечения правой и левой части неравенства, для этого найду точки . где их разность равна 0
a)x>1
тогда можно опустить знаки модуля, так как выражения в них положительны
x+1+1/(x-1)-7x=0
(x^2-7x(x-1))/(x-1)=0
x^2-7x^2+7x-=0
-6x^2+7x=0; x(7-6x)=0; x1=0( в интервал x>1 не входит)
x2=7/6-подходит. значит в этой точки графики левой и правой части пересекаются
обе функции и y1=x+1+1/(x-1) и y2=7x монотонные,
y1(2)=4; y2(2)=14-значит после пересечения в x=7/6 y2>y1. значит на интервале x=(1;7/6) y1>y2
б)x=[-1;1)
девая часть неравенства примет вид
x+1+1/-(x-1)=x+1+1/(1-x)
аналогично найду точки пересечения левой и правой части неравенства
x+1+1/(1-x)-7x=0
1-x^2+1-7x(1-x)=0
2-x^2-7x+7x^2=0
6x^2-7x+=0
D=49-48=1
x1=(7+1)/12=2/3; x2=(7-10/12=1/2-оба корня подходят для x=[-1;1)
[-1]+++(1/2)-----(2/3)++++(1)
выходит что левая часть неравенства больше правой
на x=[-1; 1/2)U(2/3;1)
в)x=(-∞;-1)
левая часть неравенства примет вид
-(x+1)+1/(-(x-1)=-x-1+1/(1-x)
найду точки пересечения левой и правой части
1/(1-x)-x-1-7x=0
(1/(1-x)-(8x+1))/(1-x)=0
1/(1-x)-(8x+1)=0
1-(8x+1)(1-x)=0
1-8x+8x^2-1+x=0
8x^2-7x=0
x(8x-7)=0
x1=0; x2=7/8-оба корня не входят в выбранный интервал x=(-∞;-1)-значит пересечения частей неравенства нет и левая часть неравенства больше правой как и на интервале x=[-1;1/2)
Ответ неравенство верно на x=(-∞;1/2)U(2/3;1)U(1;7/6)