Помогите раскрыть модуль и построить график
y=|1-|x+3||
Ответы на вопрос
Ответил nafanya2014
0
Не нужно раскрывать знак модуля.
Строим поэтапно:
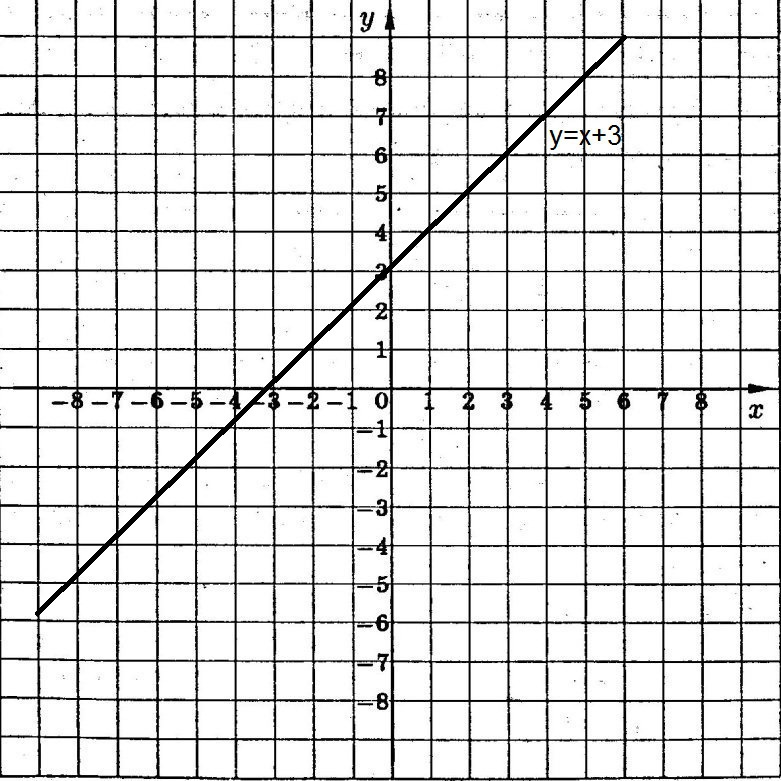
1)у = х + 3 - прямая
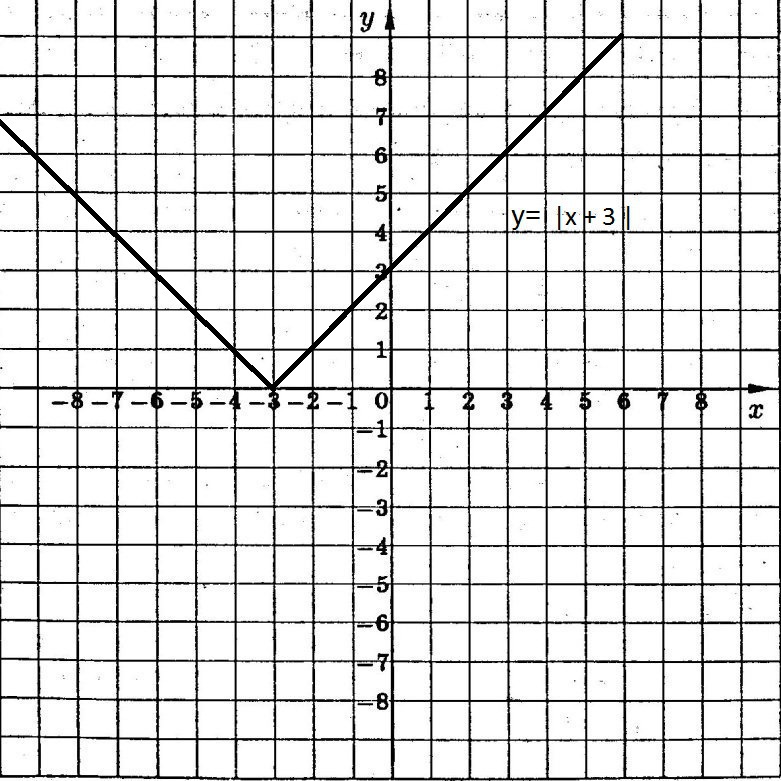
2)у = |x + 3|- отражаем часть графика, расположенную ниже оси Ох симметрично оси ох .
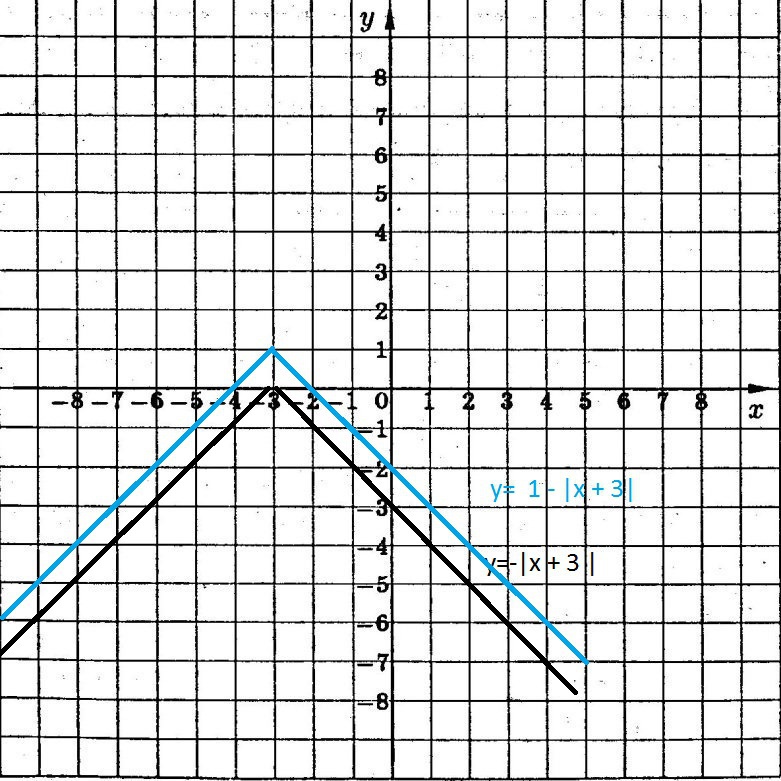
3)у= - |x + 3|- отражаем весь график y = |x + 3| симметрично относительно оси Ох.
4)у=1-|x+3| параллельный перенос графика у= - |x + 3| на 1 единицу вверх.
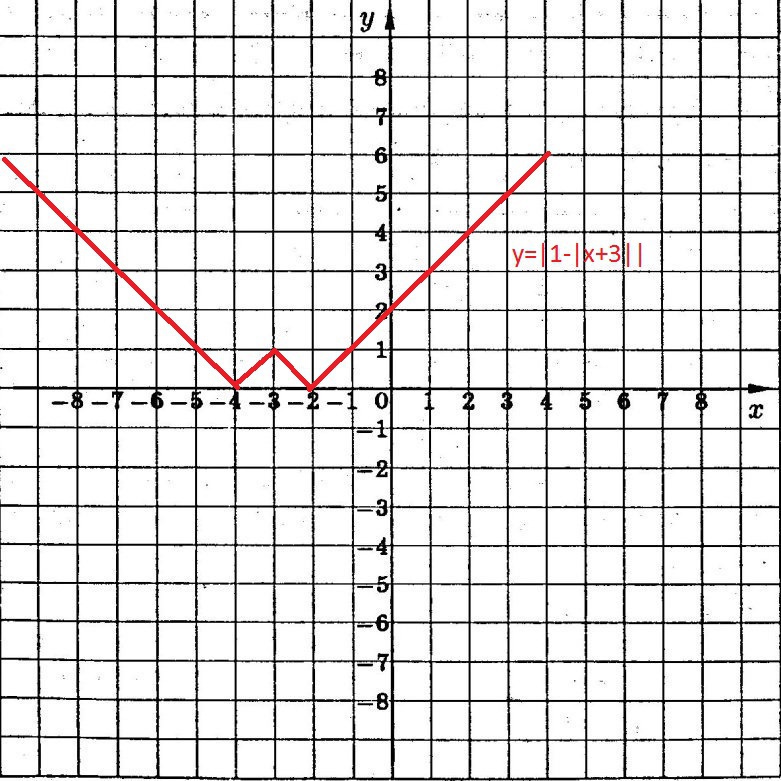
5)у=| 1 - | x + 3 || - часть графика у=1-|x+3| расположенную ниже оси Ох отражаем симметрично относительно оси ох вверх.
Раскрываем модуль
Если х+3≥0, то |x+3|=x+3
Это и означает, что при х≥-3 строим график у=х+3
Если х+3 < 0, то |x+3|=-(x+3)
Это означает, что при х < -3 строим график у=-х-3 ( отражаем симметрично оси Ох часть графика у=х+3 расположенную ниже оси Ох)
Если 1-|x+3|≥0, то есть |x+3| ≤ 1 или -1 ≤ х+3 ≤ 1 или -4 ≤x ≤ -2
|1-|x+3||=1-|x+3|
Это означает, что на [-4;-2] строим график у=1-|x+3|, который в свою очередь состоит из двух участков
На [-4;-3) |x+3|=-x-3 поэтому у=1+х+3=х+4
На [-3;-2] |x+3|=x+3 у=1-х-3=-х-2
Если 1-|x+3|< 0, то есть опять два случая
|x+3| > 1 или х+3>1
у=-1+|x+3|
На (-∞;-4) |x+3|=-x-3, поэтому у=-1-х-3=-х-4
На (-2;+∞) |x+3|=x+3, поэтому у=-1+х+3=х+2
О т в е т.
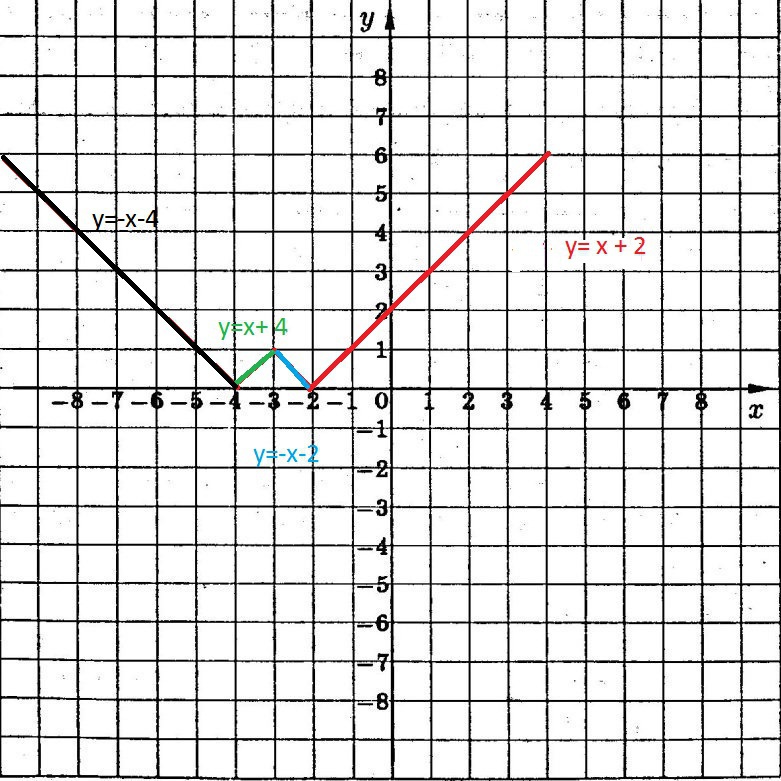
{-x-4, если х < - 4;
{x+4, если -4≤х<-3;
|1-|x+3||= {-х-2, если -3≤x≤-2;
{ x+2, если x>-2
cм. рис. 5
Строим поэтапно:
1)у = х + 3 - прямая
2)у = |x + 3|- отражаем часть графика, расположенную ниже оси Ох симметрично оси ох .
3)у= - |x + 3|- отражаем весь график y = |x + 3| симметрично относительно оси Ох.
4)у=1-|x+3| параллельный перенос графика у= - |x + 3| на 1 единицу вверх.
5)у=| 1 - | x + 3 || - часть графика у=1-|x+3| расположенную ниже оси Ох отражаем симметрично относительно оси ох вверх.
Раскрываем модуль
Если х+3≥0, то |x+3|=x+3
Это и означает, что при х≥-3 строим график у=х+3
Если х+3 < 0, то |x+3|=-(x+3)
Это означает, что при х < -3 строим график у=-х-3 ( отражаем симметрично оси Ох часть графика у=х+3 расположенную ниже оси Ох)
Если 1-|x+3|≥0, то есть |x+3| ≤ 1 или -1 ≤ х+3 ≤ 1 или -4 ≤x ≤ -2
|1-|x+3||=1-|x+3|
Это означает, что на [-4;-2] строим график у=1-|x+3|, который в свою очередь состоит из двух участков
На [-4;-3) |x+3|=-x-3 поэтому у=1+х+3=х+4
На [-3;-2] |x+3|=x+3 у=1-х-3=-х-2
Если 1-|x+3|< 0, то есть опять два случая
|x+3| > 1 или х+3>1
у=-1+|x+3|
На (-∞;-4) |x+3|=-x-3, поэтому у=-1-х-3=-х-4
На (-2;+∞) |x+3|=x+3, поэтому у=-1+х+3=х+2
О т в е т.
{-x-4, если х < - 4;
{x+4, если -4≤х<-3;
|1-|x+3||= {-х-2, если -3≤x≤-2;
{ x+2, если x>-2
cм. рис. 5
Приложения:
Новые вопросы