помогите пж даю много баллов
Приложения:
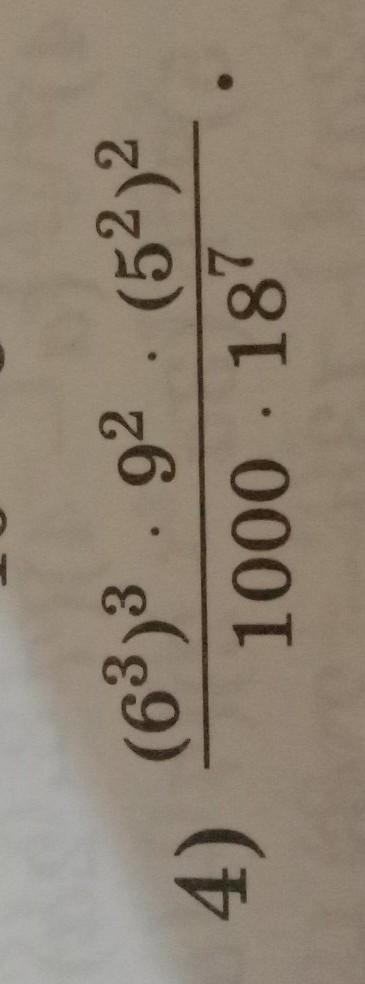
Ответы на вопрос
Ответил kamilmatematik100504
0
Ответ:
Объяснение:
Решение :
Приложения:

Новые вопросы