Алгебра, вопрос задал vika2345612 , 6 лет назад

ПОМОГИТЕ ПРОШУ
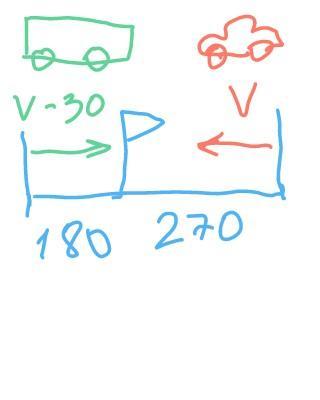
. Из двух городов одновременно навстречу друг другу выехали автомобиль и автобус. Автомобиль до встречи проехал 270, а автобус — 180 км. Найдите скорость автомобиля, если она на – 30 км/ч больше скорости автобуса.

Ответы на вопрос

Ответил spasibo3pajbrh

Пусть искомая скорость автомобиля = V

Тогда по условию скорость автобуса =V-30

Время, которое потратит автобус на путь до встречи с автомобилем будет определяться

частному пройденного пути и скорости автобуса:

$t _{автобус}= \frac{180}{v - 30}$

Для автомобиля же это время будет

$t_{автомобиль} = \frac{270}{v} </p><p>$

Так как до встречи автомобиль и автобус проехали одинаковое время, то

$</p><p>t_{автобус}=t_{автомобиль}$

поэтому:

$\frac{180}{v - 30} = \frac{270}{v}$

решаем:

$\frac{2 \times 90}{v - 30} = \frac{3 \times 90}{v} \\ \frac{2}{v - 30} = \frac{3}{v} \\ 2v = 3v - 90 \\ v = 90$

Ответ: Скорость автомобиля =90 км/ч

Приложения:

Новые вопросы

Технология, 1 год назад

Русский язык, 1 год назад

Физика, 6 лет назад

Математика, 6 лет назад

Литература, 8 лет назад

Физика, 8 лет назад