Алгебра, вопрос задал iliasparov , 2 года назад

Помогите пожалуйста задание за фото

Приложения:

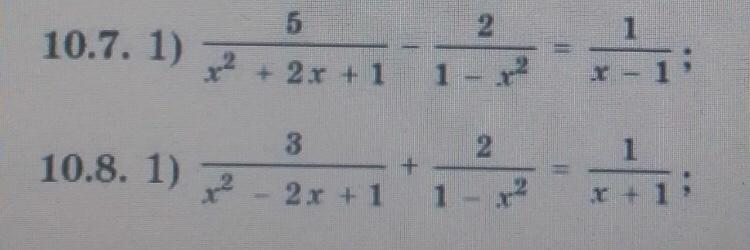
Ответы на вопрос

Ответил Аноним

Ответ:

Первое х=4

Второе х=4

iliasparov: Можно с решением пожалуйста:)

Ответил karenananyan2017

Ответ:

10.7

$\frac{5}{x^{2} +2x+1}-\frac{2}{1-x^{2} }=\frac{1}{x-1} \\\\\frac{5}{(x+1)^{2} }-\frac{2}{(1-x)(1+x) }-\frac{1}{x-1}=0 \\\\\frac{5}{(x+1)^{2} }+\frac{2}{(x-1)(1+x) }-\frac{1}{x-1}=0\\\\\frac{5(x-1)+2(x+1)-(x+1)^{2} }{(x-1)(x+1)^{2} }=0\\\\\frac{5x-5+2x+2-(x^{2}+2x+1 ) }{(x-1)(x+1)^{2} }=0\\\\\frac{-x^{2} +5x-4}{(x-1)(x+1)^{2} }=0\\\\\frac{-x^{2} +4x+x-4}{(x-1)(x+1)^{2} }=0\\\frac{-x(x-4)+x-4}{(x-1)(x+1)^{2} }=0\\\\$

$\frac{(x-4)(-x+1)}{(x-1)(x+1)^{2} }=0\\\\\frac{(x-4)(-(x-1))}{(x-1)(x+1)^{2} }=0\\\\-\frac{x-4}{(x+1)^{2} }=0$

x будет 0 только когда в числите будет ноль⇒x-4=0

x-4=0

x=4

10.8

$\frac{3}{x^{2} -2x+1}+\frac{2}{1-x^{2} }=\frac{1}{x+1} \\ \\\frac{3}{(x-1)^{2} }+\frac{2}{(1-x)(1+x) }-\frac{1}{x+1}=0 \\\\\frac{3}{(x-1)^{2} }-\frac{2}{(x-1)(1+x) }-\frac{1}{x-1}=0\\\\\frac{3(1+x)-2(x-1)-(x-1)^{2} }{(x-1)^{2} (1+x)}=0\\\\\frac{3+3x-2x+2-(x^{2}-2x+1 ) }{(x-1)^{2} (1+x) }=0\\\\\frac{-x^{2} +3x+4}{(x-1)^{2} (1+x) }=0\\\\\frac{-x^{2} +4x-x+4}{(x-1)^{2} (1+x) }=0\\\\\frac{-x(x-4)-(x-4)}{(x-1)^{2} (1+x) }=0\\\\\frac{-(x-4)(x+1)}{x-1x^{2}(1+x) }\\\\\frac{-(x-4)}{(x-1)^{2} }$