Алгебра, вопрос задал Astapenko1593 , 11 месяцев назад

Помогите пожалуйста. Вычислить пределы функций, не пользуясь средствами
дифференциального исчисления.

Приложения:

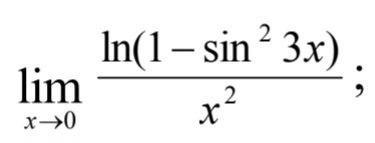
Ответы на вопрос

Ответил NNNLLL54
0

Ответ:

Применяем замену бесконечно малых величин эквивалентными .

 \bf ln\, (1+\alpha (x))\sim \alpha (x)\ \ ;\ \ \sin\, \alpha (x)\sim \alpha (x)\ \ ,\ \ \ \alpha (x)\to 0  

\bf \lim\limits_{x \to 0}\, \dfrac{ln\, (1-sin^23x)}{x^2}=\lim\limits_{x \to 0}\, \dfrac{-sin^23x}{x^2}=\lim\limits_{x \to 0}\, \dfrac{-(3x)^2}{x^2}=\lim\limits_{x \to 0}\, \dfrac{-9x^2}{x^2}=-9  

Приложения:
Предыдущий вопрос
Следующий вопрос
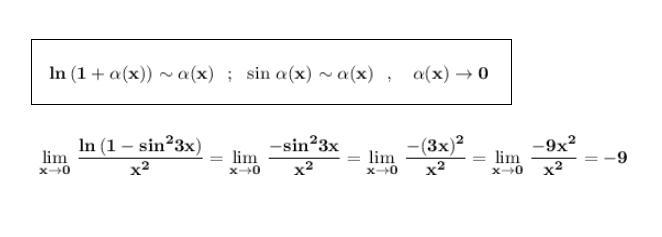
Новые вопросы
Математика, 11 месяцев назад
X+265=673-199 вычислить...
Қазақ тiлi, 11 месяцев назад
ТЫНДАЛЫ 2-тапсырма. Мәтінде жауабы бар нұсқаны белгіле. А) Парламент Ақмола қаласын «Астана» деп ауыстыру туралы ұсынысты қашан қабылдады? ә) Кімдер астананы өзінің туған қаласы санайды? Б)...
Английский язык, 11 месяцев назад
4. Ex. 5,6 p. 19 Answer the questions 1. What sport does Martha do? 2. How old is Martha? - ... 3. Where is the court? - .... 4. What does she want to be one day? - . 5. What has her sport got?
Физика, 11 месяцев назад
Яка кількість теплоти необхідна, щоб розплавити 375 г золота, взятого при температурі 35 ℃. СРОЧНО ДАЮ 10 БАЛЛОВ...
География, 6 лет назад
Что это ?даю 10 балов за правильны...
Другие предметы, 6 лет назад
Aşağıdaki sorunun cevabını verilen boşluğa yazınız. bilimin gelişmesinde Islam dininin ilim öğrenmeye ve özgür düşünceye verdiği destek önemli islamiyet ile bilimsel çalışmalar "Altın Çağ"ını...