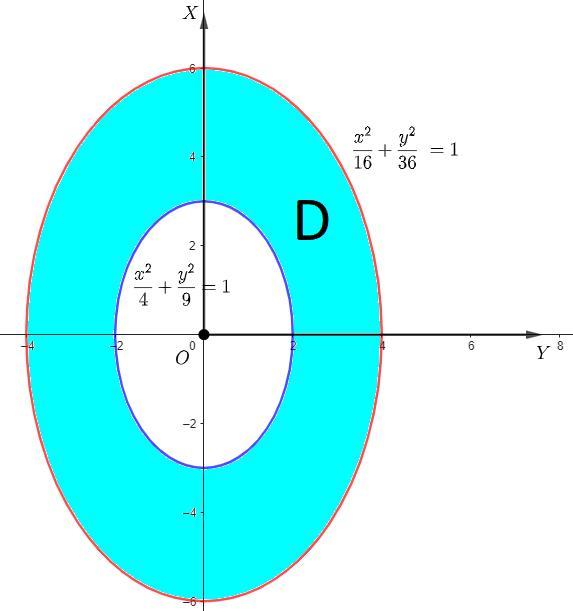
Математика, вопрос задал Reideen , 1 год назад

Помогите, пожалуйста, вычислить двойной интеграл по области D:
$\displaystyle \int\limits {\int\limits {\bigg(\frac{x^2}{4}+\frac{y^2}{9} \bigg)} \, dx } \, dy ; \;\;D: \; \frac{x^2}{4}+\frac{y^2}{9}=1, \; \frac{x^2}{16}+\frac{y^2}{36}=1$
Так понимаю, что надо переходить к эллиптической полярной СК, но никак не могу понять, какие брать пределы интегрирования.

Ответы на вопрос

Ответил mathkot

Ответ:

$\boldsymbol{\boxed{ \iint\limits_{D} {\bigg(\frac{x^{2} }{4} +\frac{y^{2} }{9} \bigg)} \, dxdy = 45\pi }}$

Примечание:

Обобщенные полярные координаты задаются следующим соотношением:

Где обобщенные полярные координаты $(r; \phi)$ связанны с декартовыми координатами $(x;y)$ следующими соотношениями:

$\displaystyle \left \{ {{x = ar \cos \phi} \atop {y = br \sin \phi}} \right.$

Где:

$r \geq 0$

$\phi \in [0;2\pi]$

$a,b > 0;a \neq b$

Якобиан преобразования координат:

$\det \bigg(\dfrac{\partial(x;y)}{\partial(r;\phi)} \bigg) = abr$

Уравнение эллипса в обобщенных координатах:

$\bigg(\dfrac{x^{2}}{a^{2}} +\dfrac{y^{2}}{b^{2}} \bigg) =1$

$\dfrac{(ar \cos \phi)^{2} }{a^{2}} +\dfrac{( br \sin \phi)^{2} }{b^{2}} =1$

$\dfrac{a^{2}r^{2} \cos^{2} \phi }{a^{2}} +\dfrac{b^{2}r^{2} \sin^{2} \phi}{b^{2}} =1$

$r^{2} \cos^{2} \phi + r^{2} \sin^{2} \phi=1$

$r^{2}(\cos^{2} \phi + \sin^{2} \phi) =1$

$r^{2} =1$

(В данной системе координат координатными лучами есть эллипсы)

Двойной интеграл в обобщенных (эллиптических) полярных координатах:

$\boxed{\iint\limits_{G} {f(x;y)} \, dxdy = ab\iint\limits_{G} {f(ar \cos \phi;br \sin \phi)r} \, drd\phi}$

Переход к эллиптическим координатам может применятся когда подынтегральная функция содержит выражение $\bigg(\dfrac{x^{2}}{a^{2}} +\dfrac{y^{2}}{b^{2}} \bigg)^{k}$ .

Пошаговое объяснение:

$\displaystyle \iint\limits_{D} {\bigg(\frac{x^{2} }{4} +\frac{y^{2} }{9} \bigg)} \, dxdy$

Область $D:$

$\dfrac{x^{2} }{4} +\dfrac{y^{2} }{9} =1; \dfrac{x^{2} }{2^{2}} +\dfrac{y^{2} }{3^{2}} =1$

$\dfrac{x^{2} }{16} +\dfrac{y^{2} }{36} =1;\dfrac{x^{2} }{4^{2}} +\dfrac{y^{2} }{6^{2}} =1$

Переход к обобщенной системе координат:

$\displaystyle \left \{ {{x = 2r \cos \phi} \atop {y = 3r \sin \phi}} \right.$

$r^{2} = 1 \Longrightarrow r =\sqrt{1}=1$ - для эллипса $\dfrac{x^{2} }{2^{2}} +\dfrac{y^{2} }{3^{2}} =1$

$\dfrac{x^{2} }{4^{2}} +\dfrac{y^{2} }{6^{2}} =1$

$\dfrac{(2r \cos \phi)^{2} }{4^{2}} +\dfrac{( 3r \sin \phi)^{2} }{6^{2}} =1$

$\dfrac{4r^{2} \cos^{2} \phi }{4^{2}} +\dfrac{9r^{2} \sin^{2} \phi }{36} =1$

$\dfrac{r^{2} \cos^{2} \phi }{4} +\dfrac{r^{2} \sin^{2} \phi }{4} =1 \bigg | \cdot 4$

$r^{2} \cos^{2} \phi + r^{2} \sin^{2} \phi=4$

$r^{2}(\cos^{2} \phi + \sin^{2} \phi) =4$

$r^{2} =4 \Longrightarrow r = \sqrt{4} =2$

Двойной интеграл:

$\displaystyle \iint\limits_{D} {\bigg(\frac{x^{2} }{4} +\frac{y^{2} }{9} \bigg)} \, dxdy = 2 \cdot 3\iint\limits_{D} {r^{2} \cdot r} \, drd\phi = 6 \int\limits^{2\pi }_{0} d\phi \int\limits^{2}_{1} {r^{3}} \, dr = 6 \int\limits^{2\pi }_{0} {\frac{r^{4}}{4} \bigg|_{1}^{2}} \, d\phi =$

$\displaystyle = \frac{6}{4} \int\limits^{2\pi }_{0} {(2^{4} - 1^{4})} \, d\phi = \frac{3}{2} \int\limits^{2\pi }_{0} {(16-1)} \, d\phi = \frac{3}{2} \int\limits^{2\pi }_{0} 15 \, d\phi = \frac{3 \cdot 15}{2} \int\limits^{2\pi }_{0} d\phi = \frac{45}{2} \cdot \phi \bigg |_{0}^{2\pi} =$