Помогитe пожалуйстa важная контрольнaя
Приложения:
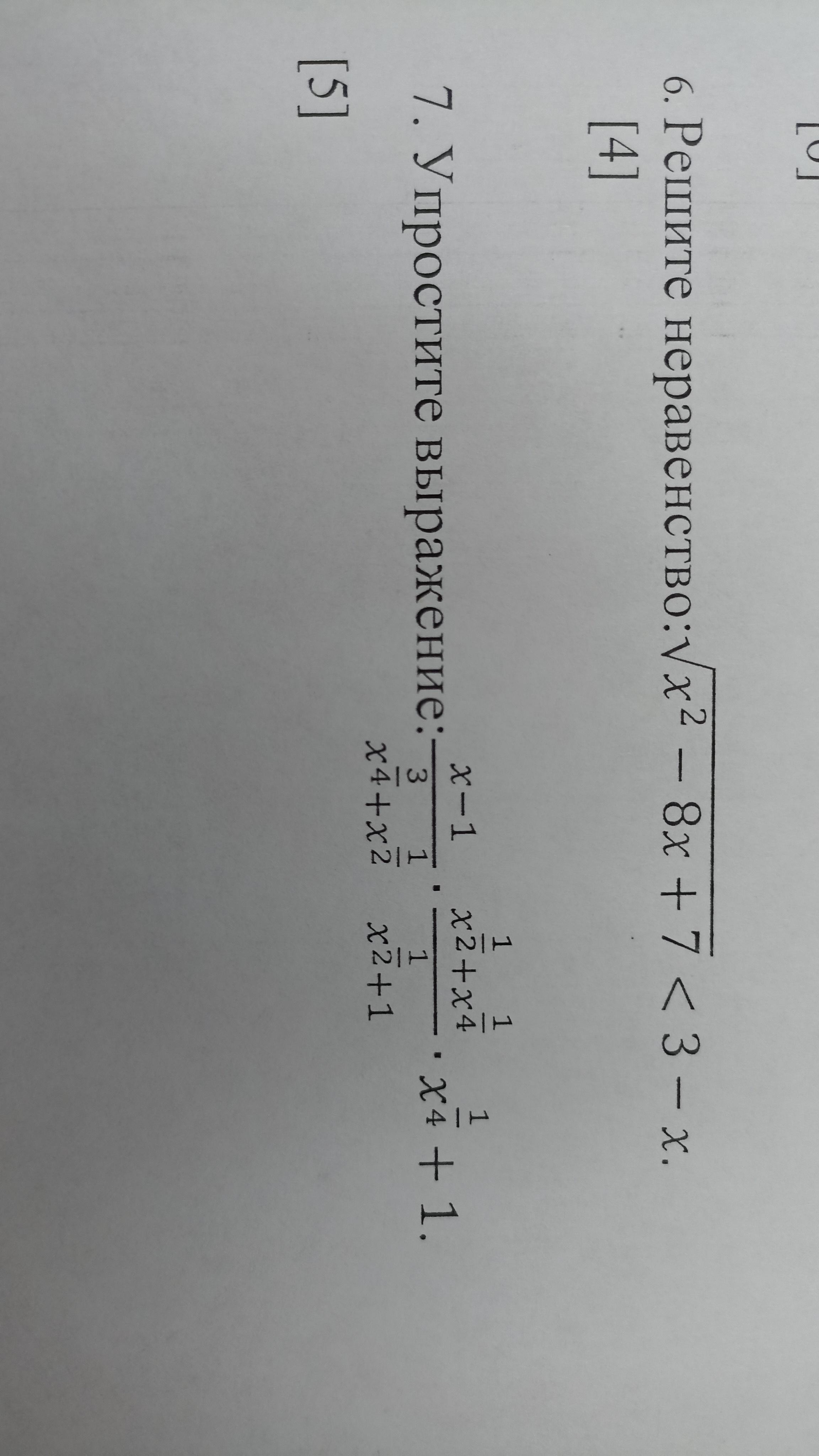
zhanibek200761:
6 задание решил, нужно 7
Ответы на вопрос
Ответил zanbolkobeev999
0
Ответ:
Объяснение:
6.
Новые вопросы
Алгебра,
6 месяцев назад
Английский язык,
6 месяцев назад
Алгебра,
11 месяцев назад
Физика,
11 месяцев назад
Английский язык,
6 лет назад
Алгебра,
6 лет назад