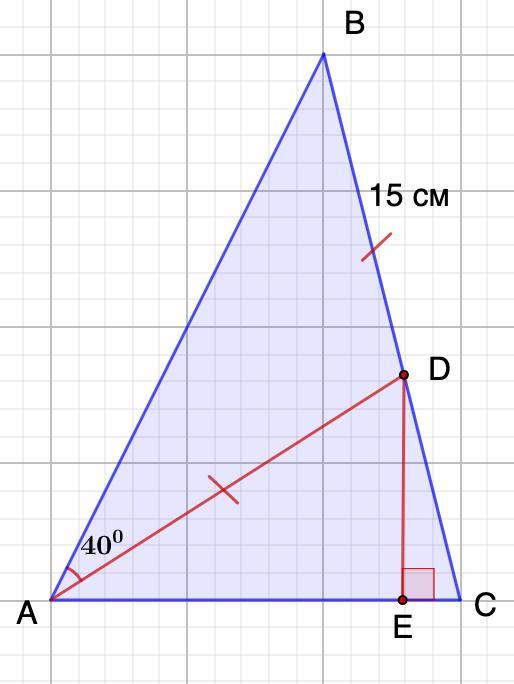
Помогите пожалуйста!!! В треугольнике ABC на стороне BC взята точка D так, что отрезки AD и DB равны 15см угол BAD=40 градусов. Из точка D на AC опущен перпендикуляр D. угол DCE на 50 градусов больше угла EDC. Найдите DE. С рисунком и объяснением пж !даю 45 баллов

Ответ:

Отрезок DE равен 7,5 см.

Объяснение:

Требуется найти  DE.

Дано: ΔАВС;

AD = DB = 15см;

∠ BAD = 40°;

DЕ ⊥ АС.

∠DCE = ∠EDC + 50°

Найти: ED.

Решение:

1. Рассмотрим ΔАВD.

AD = DB

⇒ ΔАВD - равнобедренный;

• Углы при основании равнобедренного треугольника равны.

⇒ ∠ BAD = ∠В = 40°

2. Рассмотрим ΔЕDС - прямоугольный.

Пусть ∠EDC = х, тогда ∠DCE = х + 50°

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒  ∠EDC + ∠DCE = 90°

х + х + 50° = 90°

2х = 90° - 50°   |:2

х = 20°

⇒ ∠DCE = х + 50° = 70°

3. Рассмотрим ΔАВС.

• Сумма углов треугольника равна 180°.

⇒ ∠А = 180° - ∠В - ∠DCE = 180° - 40° - 70° = 70°

4. Рассмотрим ΔАDЕ - прямоугольный.

∠DАЕ = ∠А - ∠BAD = 70° - 40° = 30°

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ DE = AD : 2 = 15 : 2 = 7,5 (см)

Отрезок DE равен 7,5 см.