помогите пожалуйста!!

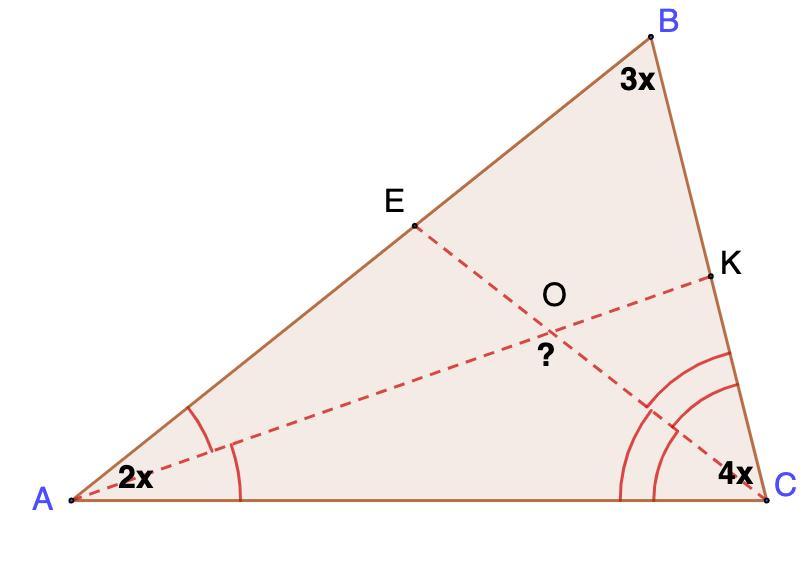
Углы треугольника АВС соотносятся как 2:3:4 Найдите угол АОС, где точка О- точка пересечения биссектрис угла А и угла С

Ответ:

Угол АОС равен 120°.

Объяснение:

Углы треугольника АВС соотносятся как 2:3:4.  Найдите угол АОС, где точка О - точка пересечения биссектрис угла А и угла С.

Дано: ΔАВС.

∠А : ∠В : ∠С = 2 : 3 : 4;

АК ∩ СЕ = 0 - биссектрисы.

Найти: ∠ АОС.

Решение:

1. Рассмотрим ΔАВС.

∠А : ∠В : ∠С = 2 : 3 : 4.

Пусть ∠А = 2х, тогда ∠В = 3х, а ∠С = 4х.

• Сумма углов треугольника равна 180°.

⇒ ∠А + ∠В + ∠С = 180°

2х + 3х + 4х = 180°

9х = 180°  

х = 20°

⇒ ∠А = 40°; ∠С = 80°

2. Рассмотрим ΔАОС.

∠ОАС = ∠А : 2 = 20° (АК - биссектриса)

∠ОСА = ∠С : 2 = 40° (СЕ - биссектриса)

⇒ ∠АОС = 180° - (20° + 40) = 120°

Угол АОС равен 120°.