Математика, вопрос задал qweennn11 , 6 лет назад

Помогите пожалуйста срочно очень
Только не так как с Photomaths! не нужно упрощать

Приложения:

orjabinina: а=у²+4у-1, тогда а+4=у²+4у+1
а(а+4)=12, а²+4а-12=0 , а₁=-6 а₂=2
1)у²+4у-1=-6 ,у²+4у+5=0........
2)у²+4у-1=2 ,у²+4у-3=0........

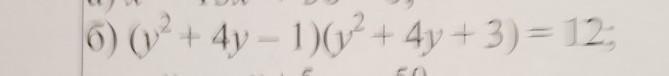
qweennn11: спасибо а можете ищё одно решить

Ответы на вопрос

Ответил Mrdenk

0

Введем новую переменную

$t = {y}^{2} + 4y - 1$

Тогда наше уравнение принимает вид

$t(t + 4) = 12$

${t}^{2} + 4t = 12$

${t}^{2} + 4t - 12 = 0$

${t}^{2} + 6t - 2t - 12 = 0$

$t(t + 6) - 2(t + 6) = 0$

$(t - 2)(t + 6) = 0$

$t = 2$

$t = -6$

Подставим и решим оба уравнения

${y}^{2} + 4y - 1 = 2$

${y}^{2} + 4y - 3 = 0$

$d = {4}^{2} - 4 \times ( - 3) \times 1 = 16 + 12 = 28$

$y = \frac{ -4 + \sqrt{28} }{2} = \frac{ - 4 + 2 \sqrt{7} }{2} = -2 + \sqrt{7}$

$y = \frac{ -4 - \sqrt{28} }{2} = \frac{ -4 - 2 \sqrt{7} }{2} = -2 - \sqrt{7}$

Теперь подставим t = -6

${y}^{2} + 4y - 1 = - 6$

${y}^{2} + 4y + 5 = 0$

$d = {4}^{2} - 4 \times 5 \times 1 = 16 - 20 = - 4$

Так как дискриминант меньше 0, то такое уравнение не имеет решений

Ответ:

$y = -2 - \sqrt{7}$

$y = - 2 + \sqrt{7}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

составьте 2 3 предложения сложных с любыми из данных слов белорусский ,киргиский, казацский ,индуский ,одеский, матроский, украинский.

Английский язык, 1 год назад

прочитай текст и выбери подходящий по смыслу слова...

Қазақ тiлi, 6 лет назад

Ответь на вопросы Даю 15баллов!

Математика, 6 лет назад

Помогите пожалуйста срочно очень ...

Математика, 8 лет назад

x-2=2x-33 Решите пожалуйста!

Алгебра, 8 лет назад

решить уравнение (2x-3)^2=(1-2x)^2...