помогите, пожалуйста, срочно!
Найти общее решение дифференциального уравнения
Приложения:
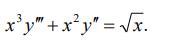
Ответы на вопрос
Ответил NNNLLL54
1
Ответ:
Новые вопросы