Помогите пожалуйста срочно надо)до вечера помогите!!!!!! кто может пожалуйста
Приложения:

Ответы на вопрос
Ответил 90misha90
0
1) для того, что бы функция могла оказаться парной или не парной, ее область определения должна быть симметричной относительно начала координат.
Единственным не симметричным интервалом, относительно начала координат есть интервал![[-5;6] [-5;6]](https://tex.z-dn.net/?f=%5B-5%3B6%5D)
Ответ: 3)![[-5;6] [-5;6]](https://tex.z-dn.net/?f=%5B-5%3B6%5D)
2)

Ответ: 3)
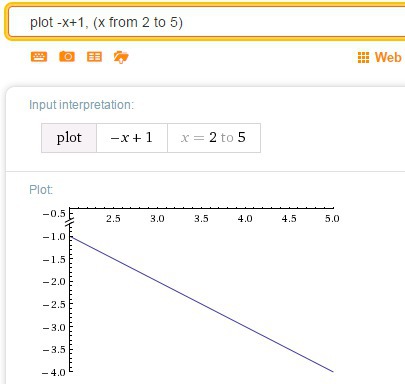
3) Графиком функции есть прямая, и эта функция является монотонно убывающей на всей области действительных чисел в силу отрицательного коэффициента перед
есть прямая, и эта функция является монотонно убывающей на всей области действительных чисел в силу отрицательного коэффициента перед  , а именно
, а именно  .
.
По этому, на интервале![[2;5] [2;5]](https://tex.z-dn.net/?f=%5B2%3B5%5D)
 , а
, а 
Ответ: наибольшее: -1; наименьшее: -4
4) Числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или отрицательной), называются промежутками знакопостоянства функции.

найдем, когда функция остается положительной:



 - промежуток, который отвечает всем возможным значениям х-са, при которых данная функция остается положительной
- промежуток, который отвечает всем возможным значениям х-са, при которых данная функция остается положительной
найдем, когда функция остается отрицательной:



 - промежуток, который отвечает всем возможным значениям х-са, при которых данная функция остается отрицательной
- промежуток, который отвечает всем возможным значениям х-са, при которых данная функция остается отрицательной
5)
отдельно
Замечаем, что - это сумма бесконечно убывающей геометрической прогрессии, у которой
- это сумма бесконечно убывающей геометрической прогрессии, у которой  ,
, 
знаменатель:
По формуле суммы бесконечно убывающей геометрической прогрессии:

тогда
Ответ:
Единственным не симметричным интервалом, относительно начала координат есть интервал
Ответ: 3)
2)
Ответ: 3)
3) Графиком функции
По этому, на интервале
Ответ: наибольшее: -1; наименьшее: -4
4) Числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или отрицательной), называются промежутками знакопостоянства функции.
найдем, когда функция остается положительной:
найдем, когда функция остается отрицательной:
5)
отдельно
Замечаем, что
знаменатель:
По формуле суммы бесконечно убывающей геометрической прогрессии:
тогда
Ответ:
Приложения:
Новые вопросы