Алгебра, вопрос задал dima68880 , 6 месяцев назад

Помогите пожалуйста срочно

Приложения:

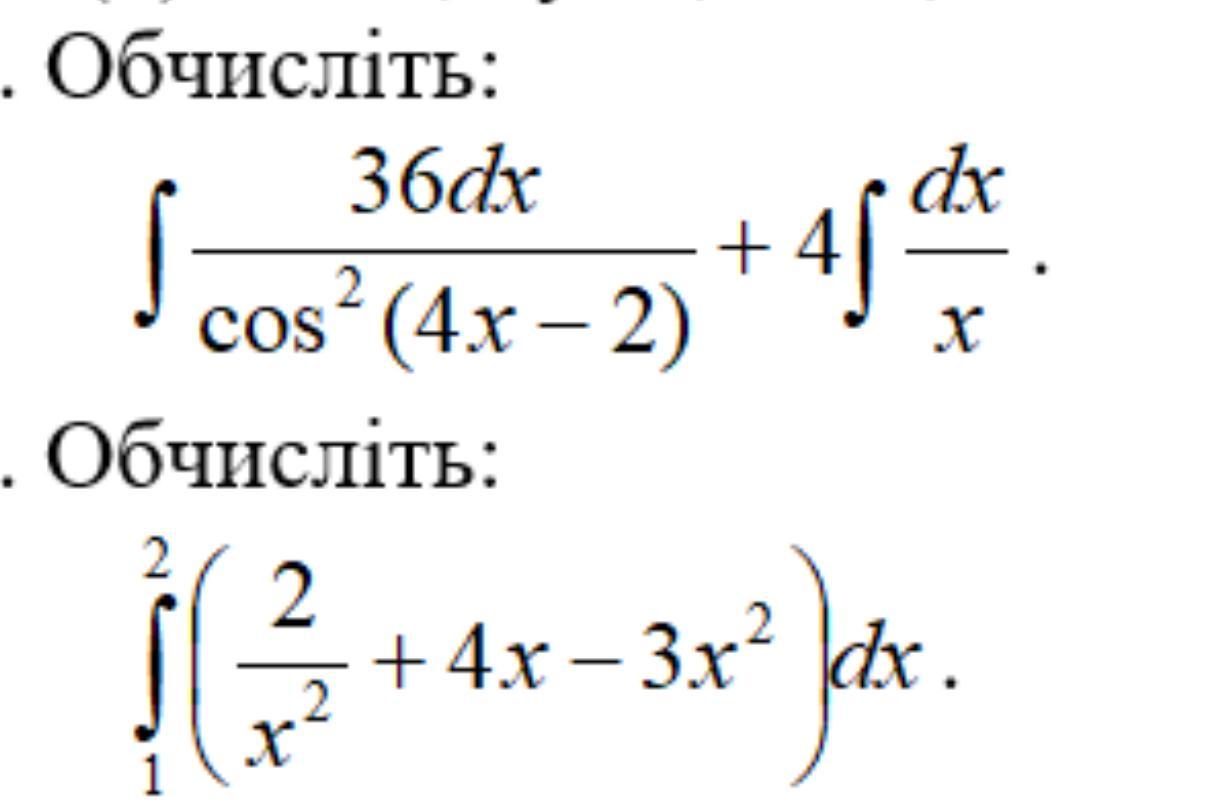
Ответы на вопрос

Ответил shadowmarder20

Відповідь:

$9tan(4x-2)+4ln|x|$ та 0

Пояснення:

Почнемо із першого прикладу:

$\int {\frac{36dx}{cos^{2}(4x-2) } } \ + 4\int{\frac{dx}{x} }$

Спробуємо розбити підінтегральні функції на множники:

$\int {\frac{1}{cos^{2}(4x-2) }*36 * dx } \ + 4\int{\frac{1}{x}dx }$

Сталий множник (36) можна виносити з під знаку інтеграла:

$36\int {\frac{1}{cos^{2}(4x-2) }dx } + 4\int{\frac{1}{x}dx }$

Тепер до першого інтеграла ми маємо використати спосіб заміни змінної (якщо ви не знаєте що це таке інтернет в допомогу, в коментарях я скинув - непогане відео )

t=4x-2, тоді dt=4. Нагадую dt - це типу похідна t (похідна ` і диференціал d - одне і теж)

$36\int {\frac{1}{cos^{2}(t) } } + 4\int{\frac{1}{x}dx }$ якщо дуже просто щоб розкрити перший інтеграл нам потрібно ще щоб було dt, воно дорівнює чотирьом, а в нас немає чотири, тому робимо ось так:

$36\int {\frac{1}{cos^{2}(t) } *1} + 4\int{\frac{1}{x}dx }$ Тепер ми розуміємо, що $1=\frac{4}{4}$ , тому робимо так:

$36\int {\frac{1}{cos^{2}(t) }* \frac{4}{4} } + 4\int{\frac{1}{x}dx }$ Ми розуміємо, що $\frac{4}{4}=\frac{1}{4}*4$ , трішки перепишемо:

$36\int {\frac{1}{cos^{2}(t) } \frac{1}{4}*4 } + 4\int{\frac{1}{x}dx }$ Винесемо $\frac{1}{4}$ за знак інтеграла, як сталий множник:

$36*\frac{1}{4} \int {\frac{1}{cos^{2}(t) } *4} + 4\int{\frac{1}{x}dx }$ І ось ми знайшли 4, яка була потрібна нам, щоб підставити замість неї dt (нагадую чому dt дорівнює 4 пише вище)

$9 \int {\frac{1}{cos^{2}(t) } dt} + 4\int{\frac{1}{x}dx }$ , ось і все: $\frac{1}{cos^2(t)}$ - це табличний інтеграл(він дорівнює tan(x)), і $\frac{1}{x}$ - теж табличний інтеграл(ln|x|), підставляємо:

$9*tan(t)+4*ln|x|$ Тепер просто замінимо t (нагадую вище ми писали t=4x-2):

$9tan(4x-2)+4ln|x|$

Тепер другий вираз:

$\int\limits^2_1 {\frac{2}{x^2}+4x-3x^2 } \, dx$ Це визначений інтеграл. Спочатку ми маємо знайти інгеграл цієї функції. Інтеграл суми дорівнює сумі інтегралів, тому перепишемо це ось так:

$\int {\frac{2}{x^2} } \, dx+ \int {4x } \, dx-\int {3x^2 } \, dx$ Спочатку виносимо сталі множники, потім користуємось таблицею інтегралів:

$2\int {\frac{1}{x^2} } \, dx+ 4\int {x } \, dx-3\int {x^2 } \, dx$

$2\int {x^{-2} } \, dx+ 4\int {x } \, dx-3\int {x^{2} } \, dx$

$2*\frac{x^{-1}}{-1} + 4*\frac{x^{2}}{2}-3*\frac{x^{3}}{3}$

$-\frac{2}{x} + 2x^{2}-3x^{3}$ - це невизначений інтеграл. А нам потрібно знайти інтеграл від одного до двох ( $-\frac{2}{x} + 2x^{2}-3x^{3} |^{2}_{1}$ ), щоб це зробити ми замість x підставляємо верхню цифру (в нашому випадку 2), і віднямаємо від цього те, що буде, якщо підставити нижню цифру (в нашому випадку 1):