ПОМОГИТЕ ПОЖАЛУЙСТА!СРОЧНО!!!
5.2. Некоторая прямая l перпендикулярна сторонам AB и AC треугольника ABC. Определите взаимное расположение прямой I и плоскости треугольних
ABC:
а) Прямая l пересекает плоскость ABC, но не перпендикулярна ей;
б) Прямая l принадлижит плоскости ABC; в) Прямая l перпендикулярна
плоскости ABC; г) Прямая l перпендикулярна плоскости ABC.
5.3. Прямая КО перпендикулярна плоскости параллелограмма ABCD. Определите прямую, перпендикулярную прямой КО.
5.4. Прямая МВ перпендикулярна сторонам АВ и ВС треугольника АВС. Найдите вид треугольника MBX, если точка X - произвольная
точка стороны АС.
Ответы на вопрос
5.2. Если прямая перпендикулярна двум пересекающимся прямым (АВ и АС) , лежащим в одной плоскости ( пл. треугольника АВС) , то эта прямая
перпендикулярна самой плоскости ( пл. ΔАВС).
в) Прямая перпендикулярна плоскости треугольника АВС.
5.3. Так как КО⊥ АВСД ( плоскости параллелограмма АВСД) , то эта прямая перпендикулярна ЛЮБОЙ прямой, лежащей в плоскости АВСД. Значит, КО⊥АВ , КО⊥ВС , КО⊥АД , КО⊥СД , КО⊥АС , КО⊥ВД ,...
5.4. МВ⊥пл ΔАВС ⇒ МВ перпендикулярна ЛЮБОЙ прямой, лежащей в этой плоскости АВС, в том числе МВ⊥ВХ ( Х∈АС⊂ΔАВС ) ⇒
∠МВХ=90° и ΔМВХ - прямоугольный .
Cм. рисунки.
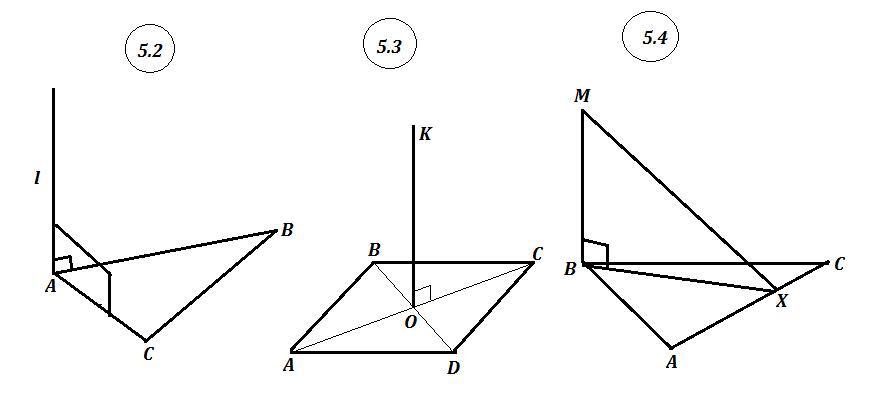
5.2. Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна самой плоскости.
l⊥(ABC)
5.3. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости.
KO⊥AB, KO⊥BC, KO⊥CD, KO⊥AD
5.4. MB⊥(ABC) => MB⊥BX, ∠MBX=90
