Математика, вопрос задал Аноним , 2 года назад

Помогите пожалуйста срочно!!!

Приложения:

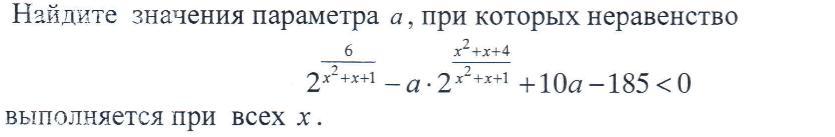
Ответы на вопрос

Ответил nafanya2014

$2^{\frac{x^2+x+4}{x^2+x+1} =2^{1+\frac{3}{x^2+x+1}}=2\cdot 2^{\frac{3}{x^2+x+1}}=2\cdot( 2^{\frac{1}{x^2+x+1}})^{3}$

$2^{\frac{6}{x^2+x+1}}=(( 2^{\frac{1}{x^2+x+1}})^{3})^2$

Замена переменной:

$( 2^{\frac{1}{x^2+x+1}})^{3}=t$

$t>0$ при любых х

Неравенство примет вид:

$t^2-2at+10a-185 <0$ (*)

D=(-2a)²-4·(10a-185)=4a²-40a+4·185=4·(a²-10a+185)

D>0

a^2-10a+185>0 при любых а, так как дискриминат квадратного трехчлена

a^2-10a+185 отрицательный: (-10)^2-4*185 <0

$t_{1}=\frac{2a-2\sqrt{a^2-10a+185}}{2}=a-\sqrt{a^2-10a+185}; \\\\ t_{2}=\frac{2a+2\sqrt{a^2-10a+185}}{2}=a+\sqrt{a^2-10a+185};$

Неравенство (*) верно при

$a-\sqrt{a^2-10a+185}<t <a+\sqrt{a^2-10a+185};$

Найдем при каких a

t > 0

$a-\sqrt{a^2-10a+185}>0$ ⇒ $a>\sqrt{a^2-10a+185}$

a^2-10a+185>0 ⇒ a> 0

Возводим в квадрат:

a^2>a^2-10a+185⇒10a>185

a>18,5

О т в е т . (18,5;+∞)

Новые вопросы

Қазақ тiлi, 1 год назад

Русский язык, 1 год назад

Математика, 2 года назад

Математика, 2 года назад

Математика, 7 лет назад

Биология, 7 лет назад