помогите пожалуйста с задачкой, тема: "треугольники"
Приложения:

Ответы на вопрос
Ответил xERISx
3
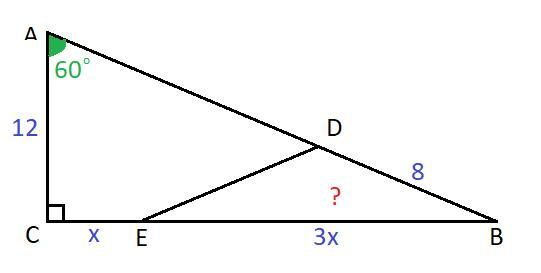
Дано : ΔABC; ∠C=90°; AC = 12;
∠BAC = 60°; BD = 8;
E∈BC; BE : EC = 3 : 1; D∈AB
Найти :
Решение :
Отношения в прямоугольном треугольнике
Сумма острых углов прямоугольного треугольника равна 90°
∠B = 90° - ∠BAC = 90° - 60° = 30°
По условию
Ответ : С) 18√3
Приложения:
david777ge:
AC =AB/2 ⇒AB=2*AC -2*12 =24 ; CB =√(AB² - AC²) =12√3 ; EB =(3/4)*CB =9√3 ; S(BDE) =(1/2)*EB *h =(1/2)*9√3 *8/2 =18√3 ( нужно было всего знать ,что длина катета против угла 30° = поовине длины гипотенузы )
Новые вопросы